周向宇院士：中國古代數學的成就

發布時間：2024-01-25

「編者按」“中國古代數學的貢獻”一文，作者係周向宇院士。在研究專(zhuan) 業(ye) 數學之餘(yu) ，作者將學習(xi) 和研究中國古代數學的心得體(ti) 會(hui) 與(yu) 研究成果整理成文，刊發於(yu) 《數學學報，中文版》2022年第4期。該文闡釋與(yu) 揭示了中國古代數學對華夏文明的貢獻，對國學、語言、文化的影響，以及對現代數學的影響與(yu) 貢獻。“數學大院”公眾(zhong) 號將陸續以推文呈現，讓讀者從(cong) 多方麵領略中國古代數學的成就與(yu) 貢獻。

1706144325(1).png

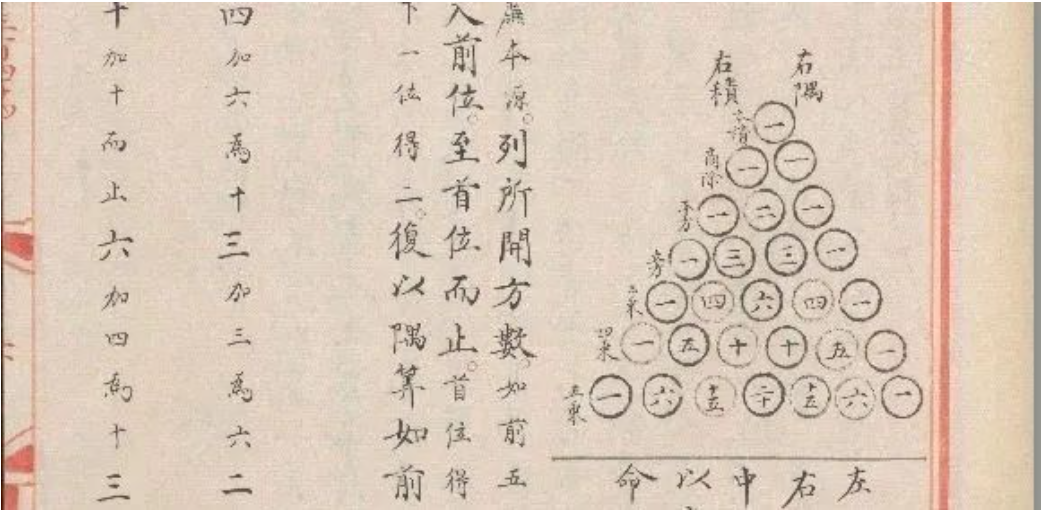
圖片來源：永樂(le) 大典.卷16343-16344.算字.明嘉靖隆慶間內(nei) 府重寫(xie) 本.劍橋大學圖書(shu) 館藏

以下內(nei) 容節選自“中國古代數學的貢獻”一文第三章“中國古代數學的成就”，作者係周向宇院士。

3.1 代數思想

中國古代很早就有了零的思想，比如在籌算中用空位表示零。零不僅(jin) 指各個(ge) 數位上的零(用空位表示，後用圓圈O)，也包括運算結果中的零。中國古代很早就引進了負數，在《九章算術》裏就很明確地引進了負數、加法的逆運算減法及其運算規則(交換律、結合律)，乘法的分配律，乘法的逆運算及分數及其運算律，這是數學發展中的一個(ge) 裏程碑。所以說，中國古代數學最早認識、發現、引進了第一個(ge) 無限群、環、域(整數群、整數環、有理數域)；另外還引進了矩陣(matrix)，發現了消元法(Gaussian elimination)，解決(jue) 了線性方程組求解問題(Cramer's Rule for system of linearequations)。

《九章算術》是一部十分重要的數學著作，總結了戰國、秦、漢時期的數學成就，西漢的張蒼、耿壽昌等曾經做過增補和整理，後來劉徽給它作了注解。雖然最後成書(shu) 於(yu) 東(dong) 漢前期(公元一世紀左右)，但許多內(nei) 容顯然早已存在於(yu) 先秦。這從(cong) 劉徽為(wei) 《九章算術》作的注就可看出。負元(逆元)、逆運算及其運算規律的引進使得運算變得方便靈活，完滿解決(jue) 了運算問題，為(wei) 抽象代數的產(chan) 生奠定了基礎。對其意義(yi) 與(yu) 價(jia) 值，套用拉普拉斯關(guan) 於(yu) 十進位值製的話來評價(jia) 是不過分的。

3.2 天元術

中國古代數學用算籌計算圓周率，開平方根、立方根和更高次的根，對多項式方程進行數值求解。此外，中國古代數學還引進了未知量“天元”，國家自然科學基金有一個(ge) “數學天元基金”，就是為(wei) 了紀念中國古代引進了變量、未知量、待定量。“宋元四傑”李冶、秦九韶、楊輝、朱世傑建立、整理和發展了天元術，而到了朱世傑時期已經發展成為(wei) 了天、地、人、物四個(ge) 變元。

在宋元四傑時期(大約為(wei) 十三、十四世紀)，中國數學的發展達到了一個(ge) 高峰，比如十進分數。比如秦九韶的大衍求一術(1247年)，這個(ge) 結果被稱為(wei) 中國剩餘(yu) 定理(高斯後來重新發現)。又比如高次方程的數值解法，也是秦九韶基於(yu) 很多古代數學家的貢獻發展總結而來的。西方在19世紀重新發現這個(ge) 方法，並稱為(wei) 霍納方法(Horner's scheme)，在前蘇聯編撰的《數學百科全書(shu) 》的相應條目“Horner's scheme”裏、

3.3 極限思想

再來談談中國古代的極限思想。《莊子·天下》有句惠子名言: “一尺之棰，日取其半，萬(wan) 世不竭。”第一天取木棰長度的，第二天取，到了第天取，萬(wan) 世都不會(hui) 窮盡。寫(xie) 成式子，即

1706145226(1).png

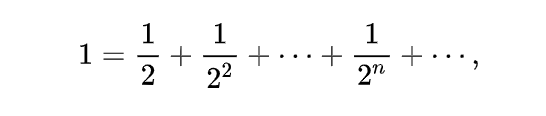
後麵必然需要省略號“......”。

另外，《墨子·經下》有句話的意思是說，一條線段從(cong) 中點分為(wei) 兩(liang) 半，取其一半再破成兩(liang) 半，仍取一半繼續分割，直到不可分割時就隻剩一個(ge) 點。《墨子·經下》：“非半弗[著斤] (編者注：該字左著右斤，讀作zhuó，因GBK編碼無法顯示該生僻字，故本文以[著斤]代替)，則不動，說在端。”這裏，[著斤](zhuó) (注：有的書(shu) 也用斫)意指：用刀斧砍。《經說下》曰：“非[著斤]半，進前取也。前則中無為(wei) 半，猶端也。前後取，則端中也。[著斤]必半，毋與(yu) 非半，不可[著斤]也”。墨子的半分法體(ti) 現了(事實上等價(jia) 於(yu) )區間套原理。半分法可以用來證明數學分析裏的幾個(ge) 重要、被認為(wei) 有難度的定理。比如證明致密性定理、聚點定理、有限覆蓋定理，還有連續函數的零點存在定理、Henstock--Kurzweil積分中的基礎---Cousin引理(對閉區間上的任一正函數，總存在閉區間的-細度分劃(-fine Perron partition)) (HK積分僅(jin) 對黎曼積分做些許改動，就蘊含了勒貝格積分)，其實用的都是墨子的半分法。

另外，惠子的取半、墨子的半分及王爾的半中說明古人應該很早就會(hui) 用尺規平分線段。

劉徽和祖衝(chong) 之的“割圓術”也蘊含了極限的思想。祖率(密率)

是非常巧妙的。祖衝(chong) 之和他的兒(er) 子祖暅編寫(xie) 了《綴術》，這本書(shu) 是唐朝算學科最難的課本。祖暅原理“冪勢既同，則積不容異”，就是說：如果兩(liang) 個(ge) 立方體(ti) 的所有等高的橫截麵積全都相等，則它們(men) 的體(ti) 積必相同(這裏“既”是“全、都”之意)。這在微積分裏被西方稱為(wei) 卡瓦列裏(Cavalieri)原理。祖暅用其原理求出“牟合方蓋”的體(ti) 積，進而得出球體(ti) 積，解決(jue) 了劉徽遺留問題。

《綴術》代表了當時數學的最高水平，但“學官莫能究其深奧，是故廢而不理”，這本書(shu) 最終失傳(chuan) 了，這是十分遺憾的事情。在我看來，《綴術》蘊含極限思想，光從(cong) 書(shu) 名來看， “綴”就有連續的含義(yi) 。

明朝數學家王文素及其《算學寶鑒》對數學有重要貢獻，比如對於(yu) 17世紀微積分創立時期出現的導數，王文素在16 世紀已發現並使用。

上述成就當然是基礎數學的成就，隻是中國古代數學的一小部分。

參考文獻

[1] 毛澤東(dong) , 改造我們(men) 的學習(xi) , 毛澤東(dong) 選集第三卷, 北京: 人民出版社, 1991:797.

[2] Cajori F., A History of Mathematical Notations, Dover Publications, Inc. New York, 1993:70.

[3] Gowers T. (Ed.), The Princeton Companion to Mathematics, Princeton University Press, 2008.

[4] 吳文俊, 對中國傳(chuan) 統數學的再認識, 百科知識, 1980年第7--8期.

[5] 程貞一, 聞人軍(jun) , 周髀算經譯注, 上海: 上海古籍出版社, 2012.

[6] 卡爾·博耶(Carl B. Boyer)著, 尤塔·梅茲(zi) 巴赫(Uta C. Merzbach)修訂, 數學史(修訂版), 中央編譯出版社, 2012.

[7] 吳文俊主編, 世界著名數學家傳(chuan) 記, 花拉子米, 北京: 科學出版社, 1995.

[8] 李文林, 數學史概覽, 北京: 高等教育出版社, 2000.