米兰体育官方网站入口是中國數學工作者的學術性法人社會(hui) 團體(ti) ,是中國科學技術協會(hui) 的組成部分。米兰体育官方网站入口的宗旨是團結廣大數學工作者,為(wei) 促進數學的發展,繁榮我國的科學技術事業(ye) ,促進科學技術人才的成長與(yu) 提高...
袁亞湘院士:黃金分割淺談
發布時間:2023-06-30
米兰体育官方网站入口第十一屆全國數學文化論壇於(yu) 2022 年 7 月 29 日 − 8 月 1 日在河南大學順利召開。米兰体育官方网站入口監事長袁亞(ya) 湘院士作大會(hui) 報告《黃金分割淺談》,以下是報告實錄。
今天我隻講數學文化的一個(ge) 小例子——黃金分割。黃金分割是在中學就接觸到的、非常初等的知識。
黃金分割比例在《幾何原本》中稱為(wei) 中末比,其定義(yi) 如下:把一條線段分成兩(liang) 段,整段比長段等於(yu) 長段比短段。歐幾裏得用幾何作圖的方法將線段分劃為(wei) 中末比。

第六章命題 30:將給定線段 (AB) 分成中末比。
歐幾裏得在沒有無理數概念的前提下,利用了很多引理通過幾何的方法得到中末比。給定一條線段 AB,如何將給定線段 (AB) 分成中末比,歐幾裏得的做法是:以 AB 為(wei) 邊在上麵畫一個(ge) 正方形 ABHC,在 AB 上找一點 E 使得以 AE 為(wei) 邊長的正方形與(yu) EB 為(wei) 邊長的四邊形 EBHF 麵積相等。
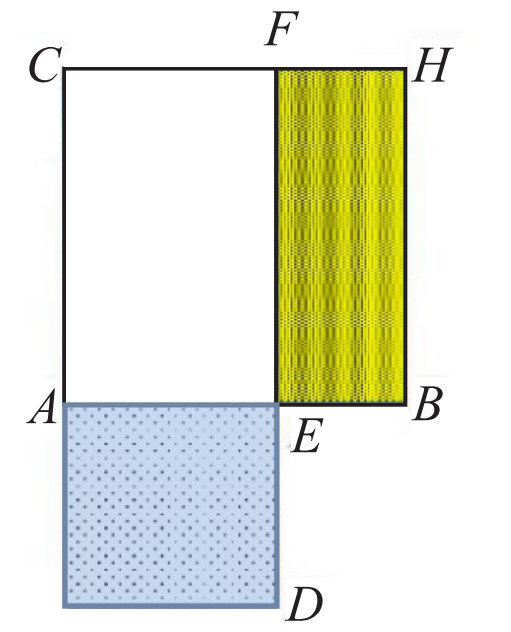
如何用幾何畫圖的方法找到具備此性質的 E ?歐幾裏得需要用到書(shu) 中的其他引理。中末比有很多神奇的性質,在《幾何原本》裏有大量命題是關(guan) 於(yu) 這個(ge) 中末比,否則歐幾裏得也不會(hui) 特意定義(yi) 這個(ge) 比例。
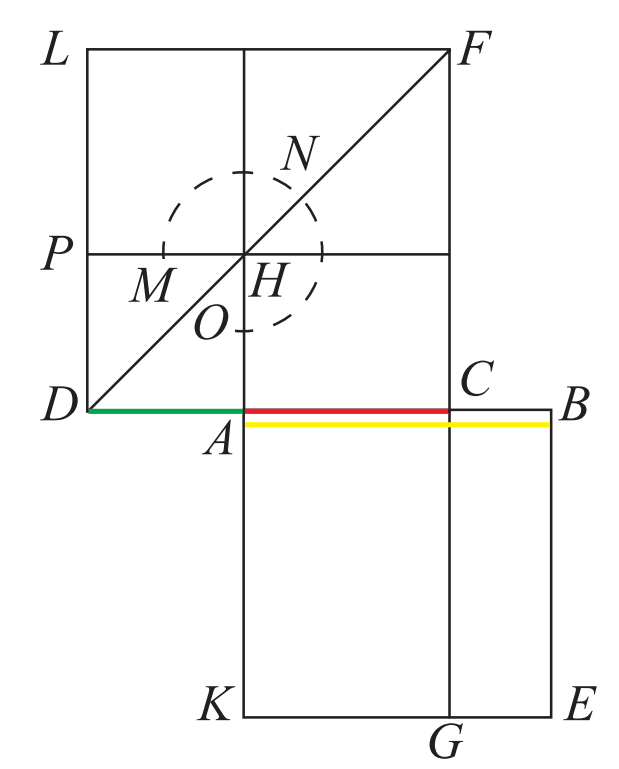
第十三章命題 1:如果把一個(ge) 線段分成中末比,則長段加整段的一半之和為(wei) 邊的正方形麵積等於(yu) 整段一半邊長的正方形的 5 倍。
現在我們(men) 用中末比的精確值就能簡單推出這一結果,但當時歐幾裏得是不知道中末比的具體(ti) 數值的。
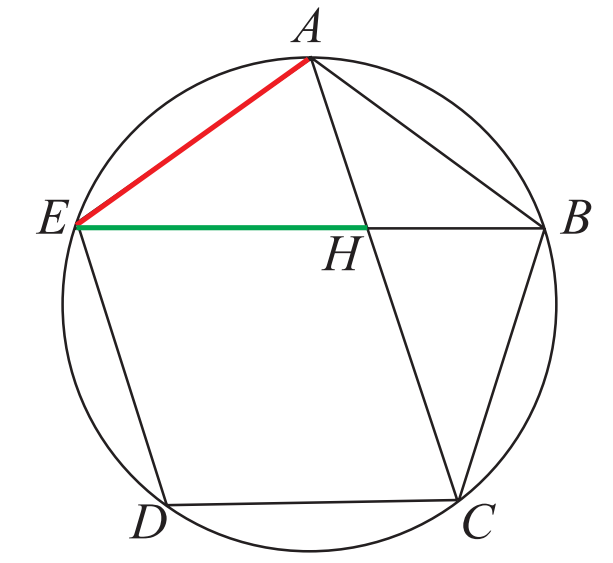
第十三章命題 8:一個(ge) 等邊等角的正五邊形,用線段順次連接兩(liang) 角,則連線交成中末比,且長段等於(yu) 五邊形的邊。
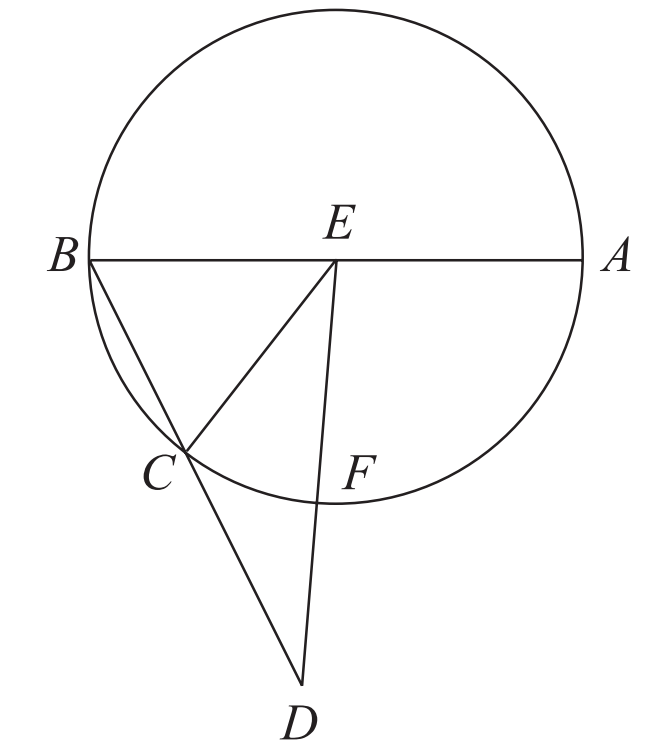
第十三章命題 9:同圓內(nei) 的內(nei) 接正六邊形的邊長與(yu) 內(nei) 接正十邊形的邊長之比是中末比。
第十三章命題 17:求作已知球的內(nei) 接十二麵體(ti) ,證明這十二麵體(ti) 的邊是稱為(wei) 餘(yu) 線的無理線段。
推論:當立方體(ti) 的一邊被分成中末比時,長段是十二麵體(ti) 的邊長。
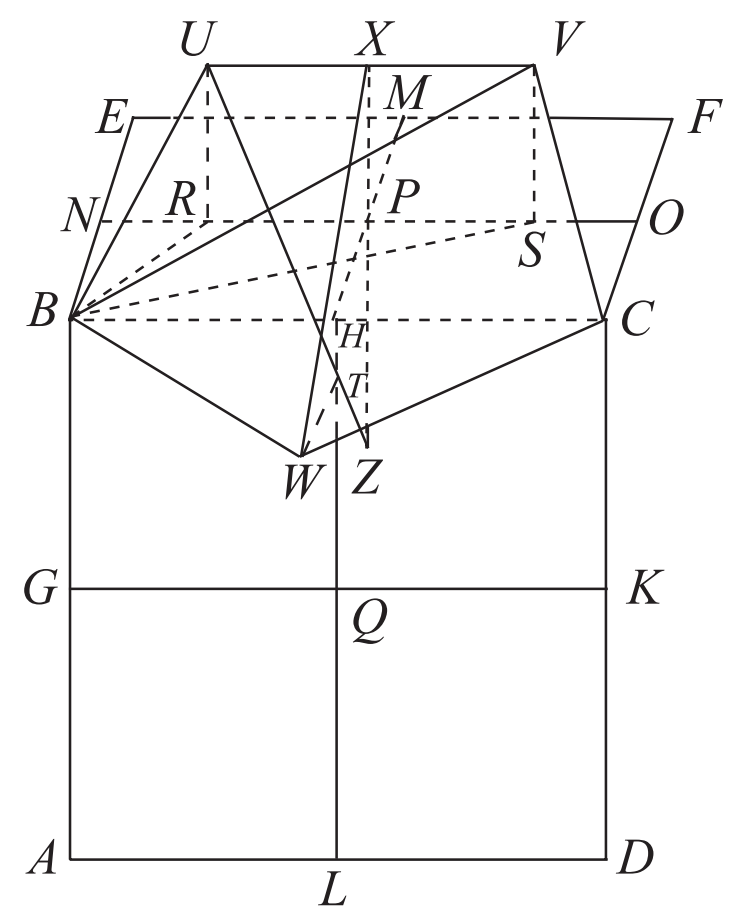
用幾何作圖的方法能得到很多這種幾何圖形。上麵這幾個(ge) 《幾何原本》中的命題都跟中末比有關(guan) 係。
16 世紀意大利著名數學家帕喬(qiao) 利的著作《神聖比例》就談到了中末比,這本書(shu) 插畫的作者是達 • 芬奇。

有很多數學家非常推崇中末比。被很多人認為(wei) 是有史以來最偉(wei) 大的數學家牛頓,提出的三大定律是基於(yu) 開普勒的三大定律。所以,毫無疑問,開普勒也是一個(ge) 偉(wei) 大的科學家。開普勒對中末比是非常推崇的,他說:幾何學有兩(liang) 大珍寶:一個(ge) 是畢達哥拉斯定理(勾股定理),另外一個(ge) 是中末比。前者可比金子,後者可稱寶玉。由此可見,中末比在幾何學中地位的重要性。
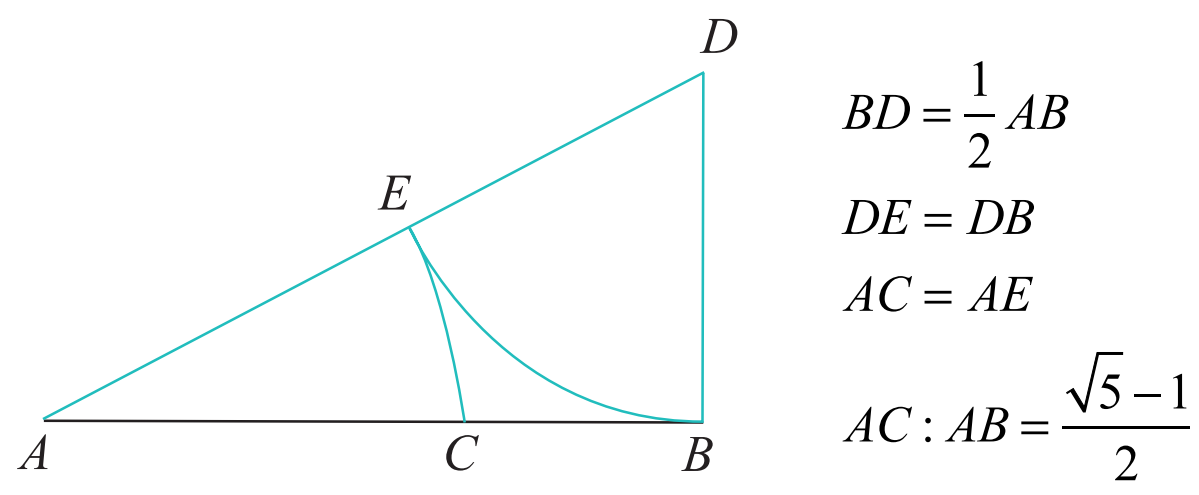
“黃金分割”這個(ge) 名字並不是由開普勒提出來的,是一位名叫歐姆的數學家命名的,他非常推崇中末比,覺得這個(ge) 比例太美好了,所以就給這個(ge) 中末比取了一個(ge) 美好的名字——黃金分割(goldener Schnitt),其中“黃金”是形容詞,指“像金子般的”,“分割”是名詞。“黃金分割”翻譯成中文應該是“像金子般的比例(分割)”,之所以用“黃金”來命名,是因為(wei) 在歐洲文藝複興(xing) 時期,人們(men) 喜歡用“金子般的”來形容事物的美好。所以“黃金分割”的意思應該是“很美好的比例”。
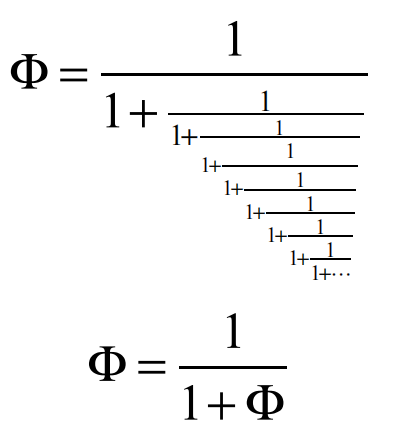
在國際上,黃金分割通常就是指中末比。 而在我們(men) 國家因曆史原因,更多的是將中末比的倒數稱為(wei) 黃金分割,這和中末比差 1,也就是把中末比小數點前麵的 1 去掉。
中末比:
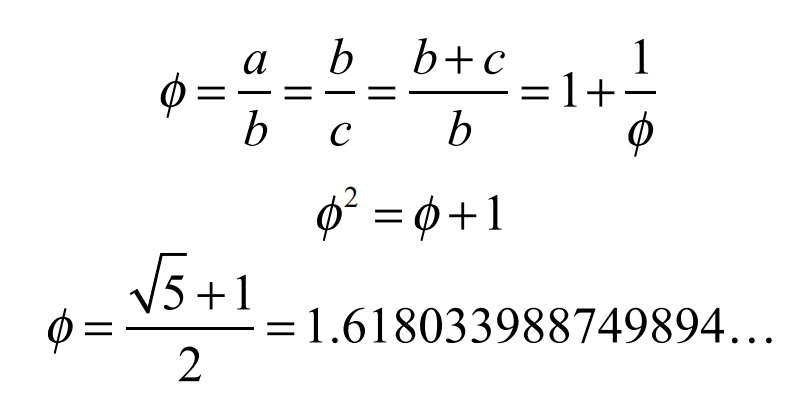
(黃金分割)黃金分割比例:
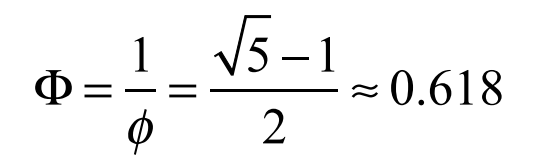
關(guan) 於(yu) 中末比有很多有趣公式,首先是它本身加 1 再開方,仍然是它本身,繼續本身加 1 再開方還是它本身,可以一直遞推下去,即如下式子:
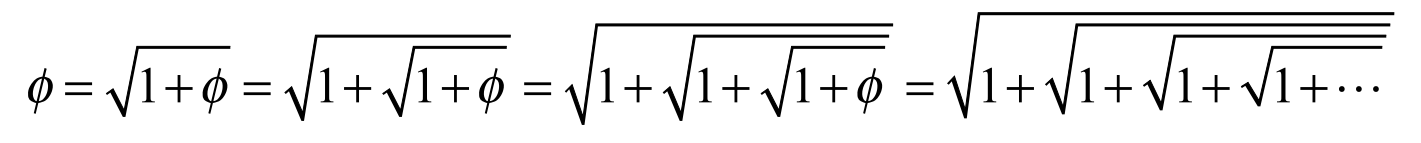
同理,也有如下形式的連分式:
1.古埃及胡夫大金字塔
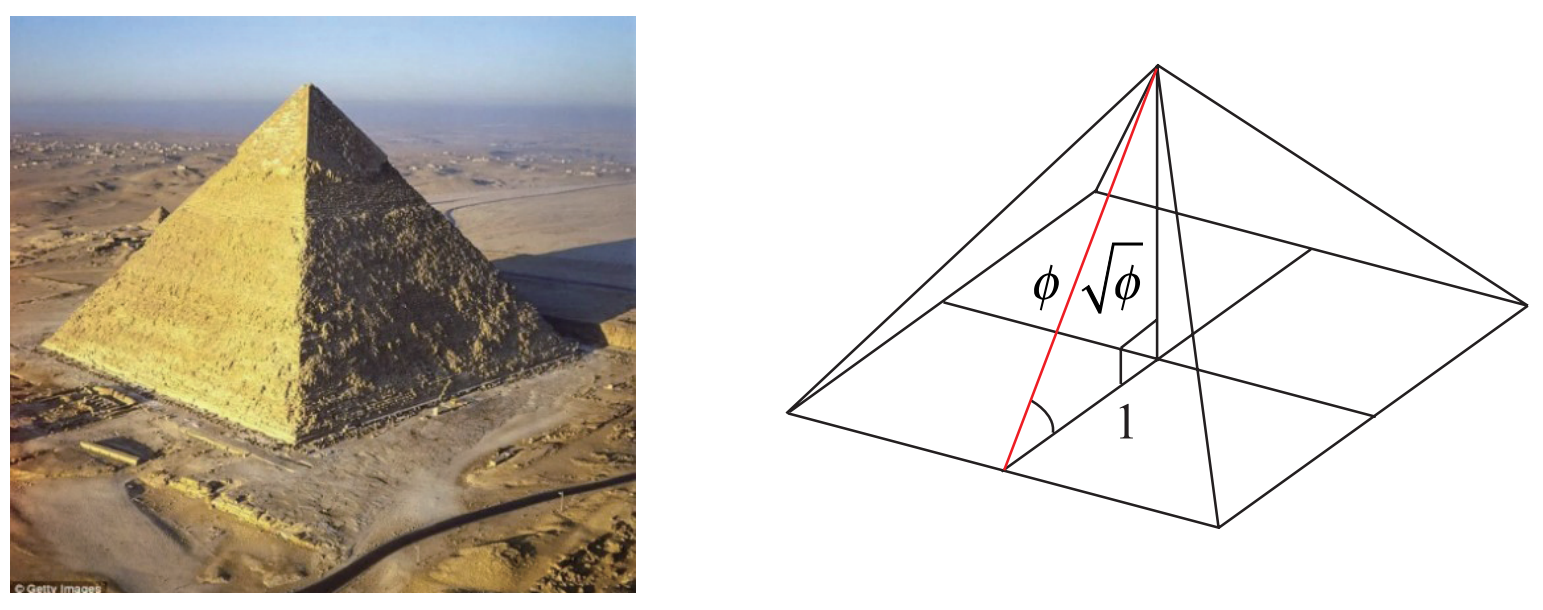
胡夫大金字塔的斜麵中線長是 611.75 英尺,斜麵底邊一半是 378 英尺 ,這兩(liang) 個(ge) 相除611.75/378≈1.618 恰好是中末比。大家可能覺得會(hui) 是巧合,但巧合一般不會(hui) 精確到小數點後四位,千分之一或萬(wan) 分之一這種精確度,所以建築師一定知道這個(ge) 中末比。
2. 雅典帕特農(nong) 神廟

雅典的帕特農(nong) 神廟,它的寬約等於(yu) 31 米,高約等於(yu) 19 米,高和寬的比例基本上非常接近於(yu) 黃金分割比例 19/31≈0.613,而且雅典帕特農(nong) 神廟存在大量黃金分割比例。由此可見,古希臘的建築師一定是數學家。
3. 巴黎聖母院、印度泰姬陵、北京電視塔、上海東(dong) 方明珠
法國巴黎著名建築巴黎聖母院,它的第一層和第二層的比例,第二層和第三層的比例都滿足中末比。印度泰姬陵裏的一些布局、北京電視塔(238/386.5≈0.616)、上海東(dong) 方明珠(289.2/468≈0.618)都存在黃金分割比。


著名畫家達•芬奇也是一位數學家,《維特魯威人》的底稿中有很多線段都滿足黃金分割比。
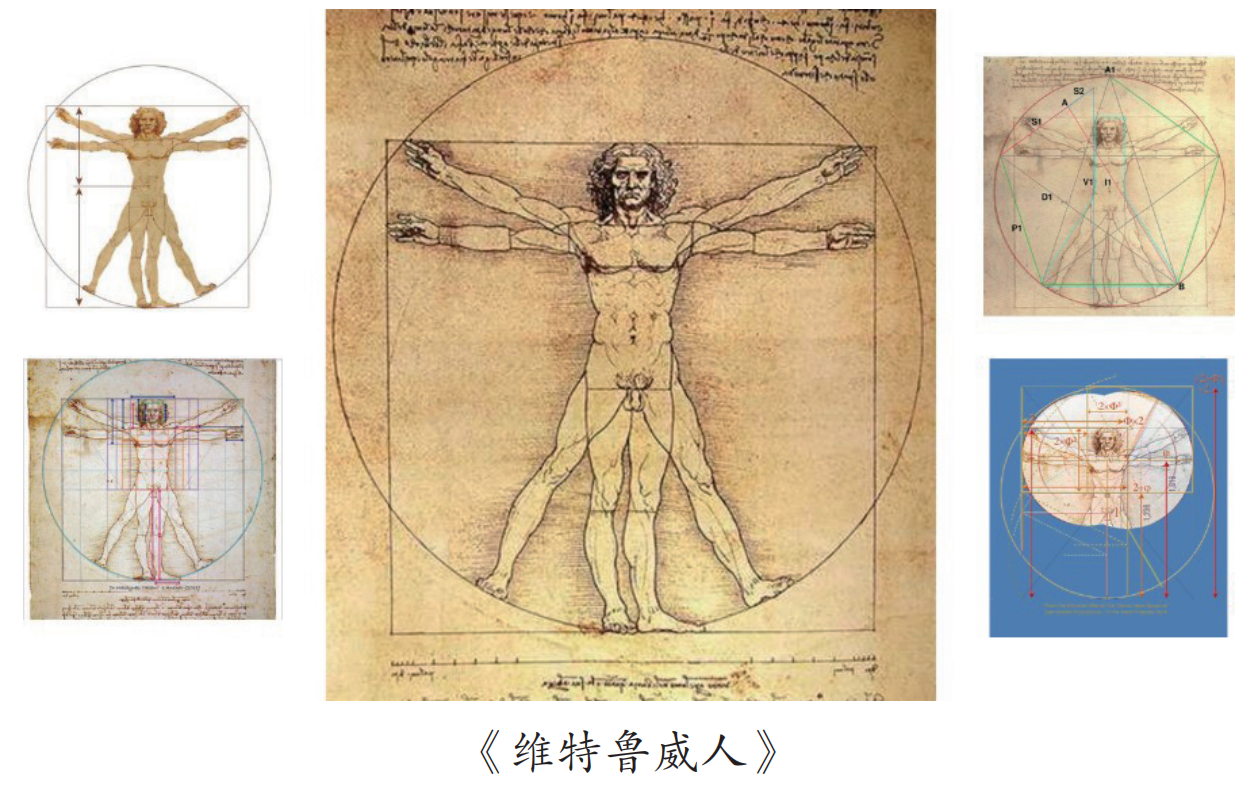
名畫《蒙娜麗(li) 莎》存在大量的黃金分割比例;《最後的晚餐》這幅畫的布局、畫中建築背景的分劃都用到了黃金分割比例


著名畫家米開朗基羅《創世紀》的布局同樣用到了黃金分割比例。

印象派畫家修拉的《安涅爾浴場》中整個(ge) 畫麵的布局、海岸線高度、人物位置的布局都遵循黃金分割比例。

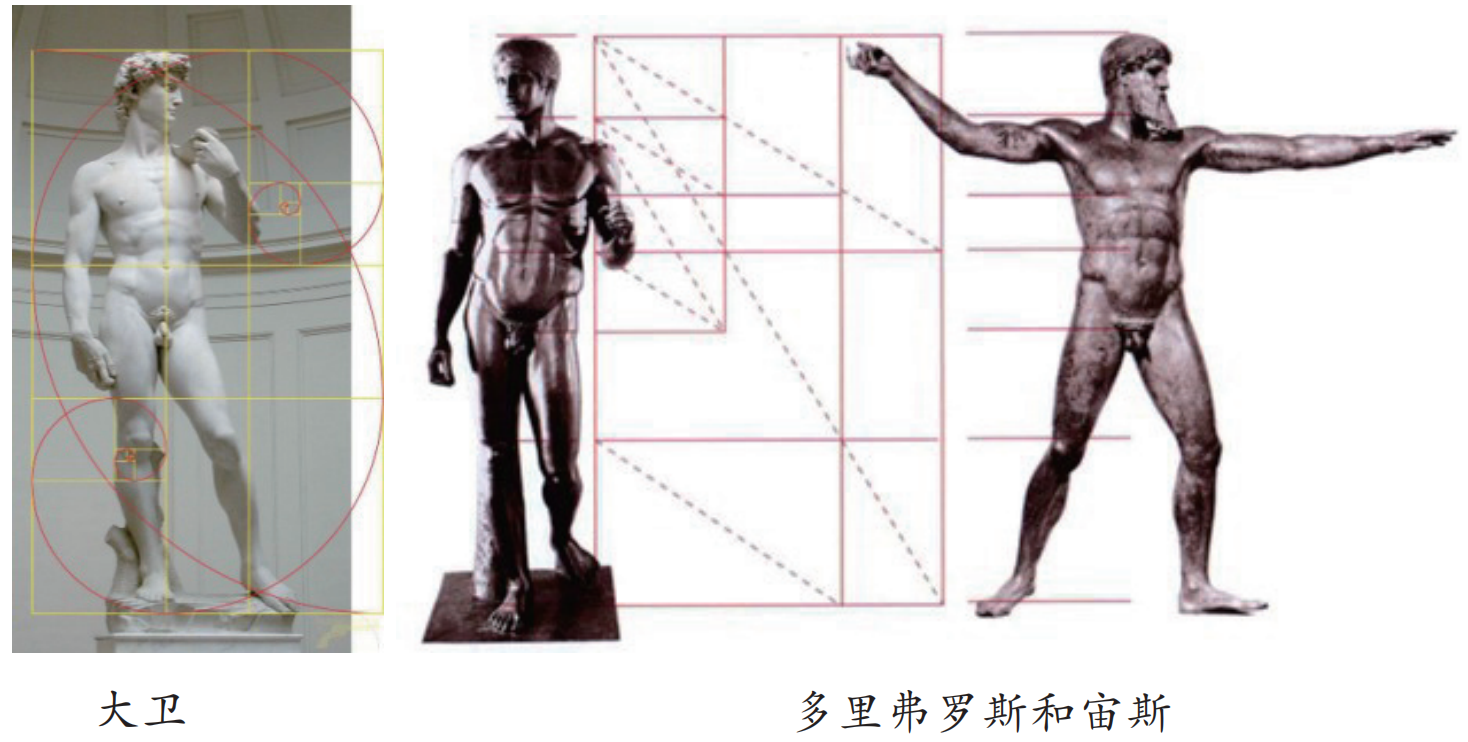
號稱世界最美雕塑——維納斯,她從(cong) 腳下到肚臍的高度跟整個(ge) 雕塑的高度符合黃金分割比。同樣涉及黃金分割比的雕塑還有《大衛》、《多裏弗羅斯》和《宙斯》。

在音樂(le) 方麵,貝多芬的第五交響曲,它的第一樂(le) 章按照主題部分和再現部分成兩(liang) 部分,前麵主題部分有 377 音節,後麵再現部分有 233 音節,233/377≈0.618,所以貝多芬他在布局自己第一樂(le) 章的兩(liang) 部分時完全是選擇了滿足黃金分割比例。

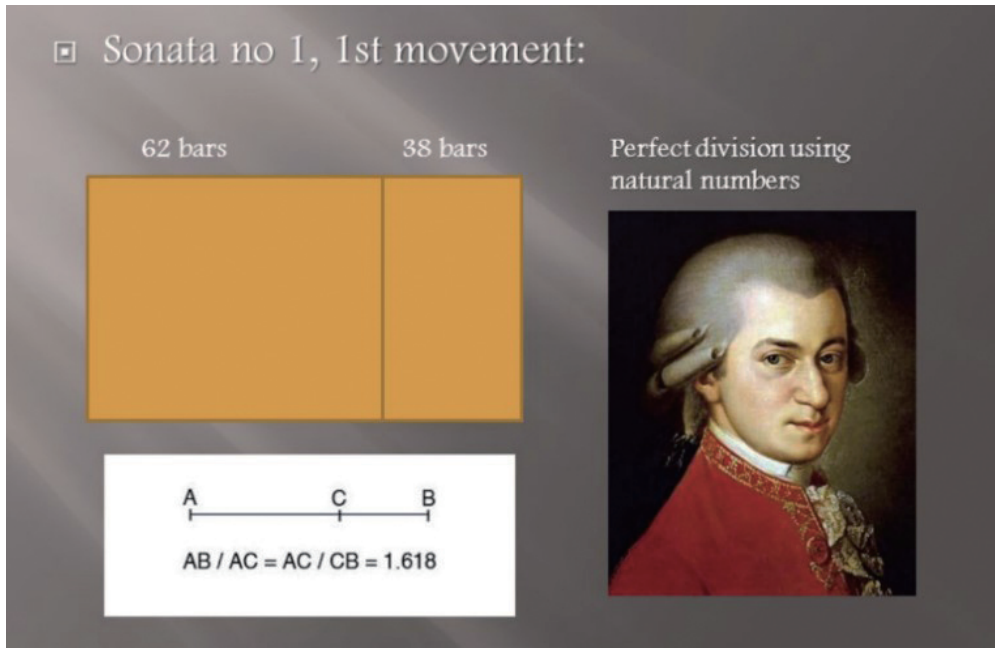
將莫紮特《第 1 鋼琴奏鳴曲》的第一樂(le) 章分成兩(liang) 部分:前麵主題部分和後麵再現部分。前麵主題部分是62 小節,後麵再現部分是38 小節,這兩(liang) 部分的比例為(wei) 0.613,也是黃金分割比。
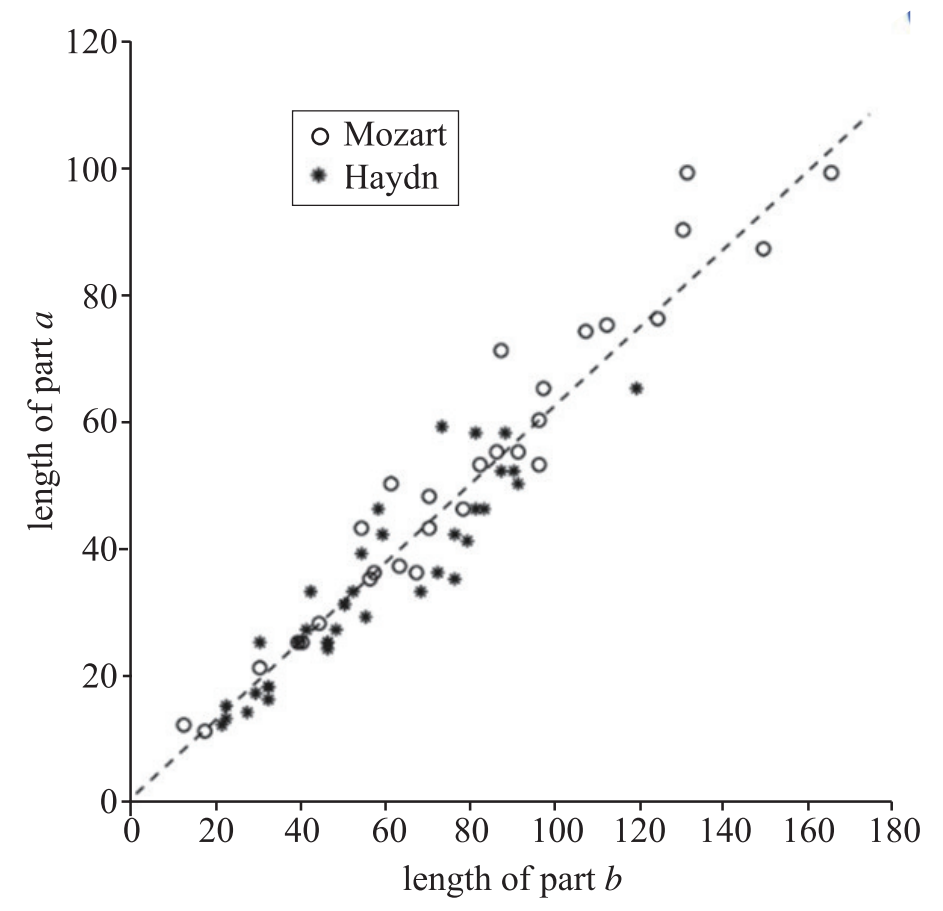
J. Ryden 在論文《Statistical Analysis of Golden-Ratio in Piano Sonatas by Mozart and Haydn》中對所有的奏鳴曲(莫紮特、海頓)進行統計,並畫了一條 0.618 斜線,發現第一樂(le) 章主題部分跟再現部分音節比例基本上都落到這條直線附近,也就是基本上這兩(liang) 段的比都接近於(yu) 0.618,可見,音樂(le) 家在寫(xie) 樂(le) 章的時候,這種比例最舒服。
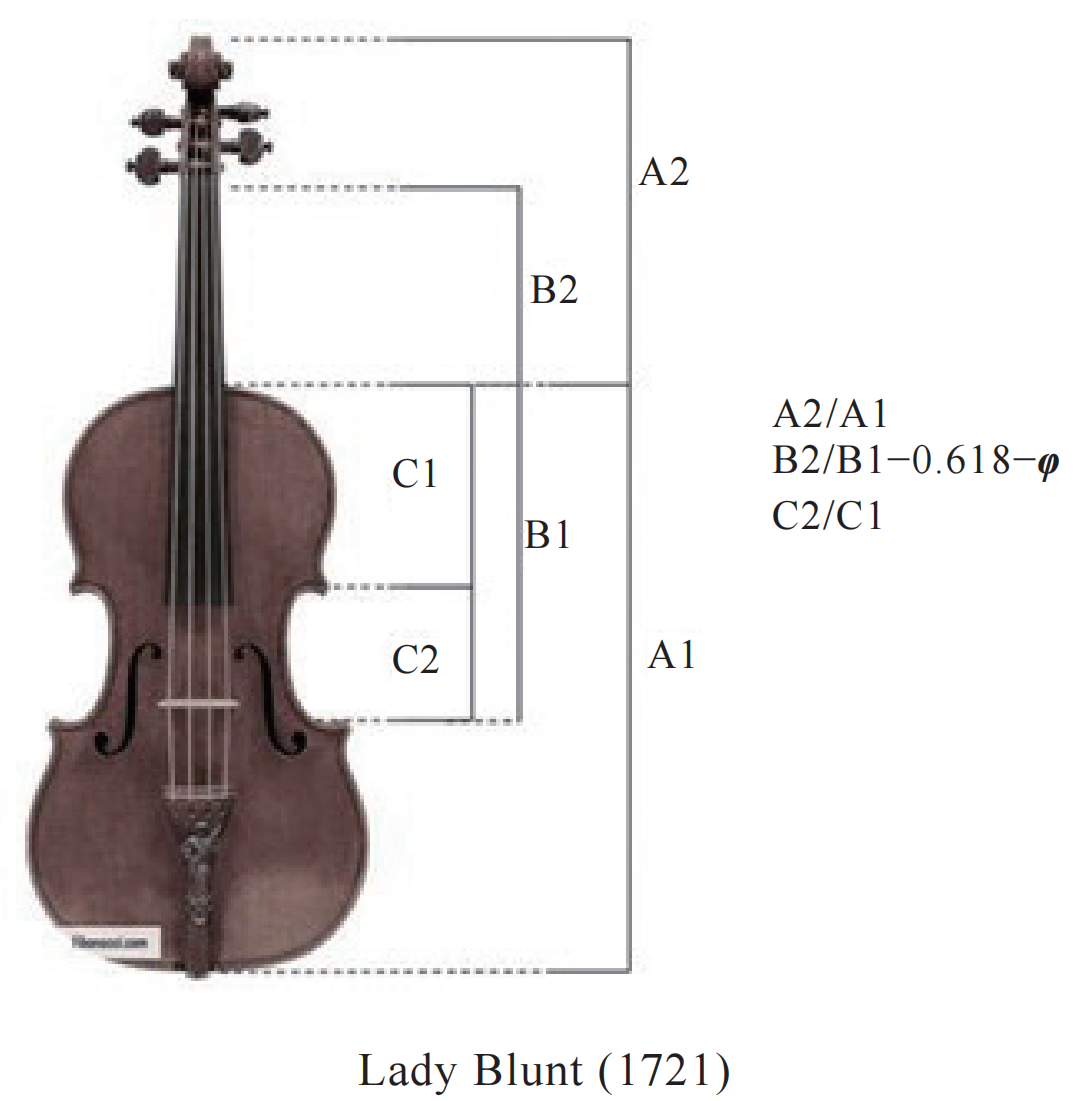
樂(le) 器上也存在黃金分割。著名小提琴 Lady Blunt (1721) 是 18 世紀小提琴製作大師Antonio Stradivari 製作。關(guan) 於(yu) 這把小提琴之所以命名為(wei) Lady Blunt, 是因為(wei) Lady Blunt(她是拜倫(lun) 孫女的女兒(er) )曾收藏它達 30 年。該小提琴 2011 年拍賣成交價(jia) 高達1000 萬(wan) 英鎊。這把小提琴不僅(jin) 音質好,有趣的是它在形狀設計上,各個(ge) 部分有很多是滿足黃金分割比例。
黃金分割在自然界也是大量存在的。奧黛麗(li) • 赫本臉部各部分比例符合黃金分割比,由此可見,不僅(jin) 達芬奇畫中的美人“蒙娜麗(li) 莎”存在黃金分割比,現實生活中大家公認的美人“奧黛麗(li) • 赫本”長相也符合這個(ge) 比例。

大自然中的螺和玫瑰長相也符合黃金分割比例。
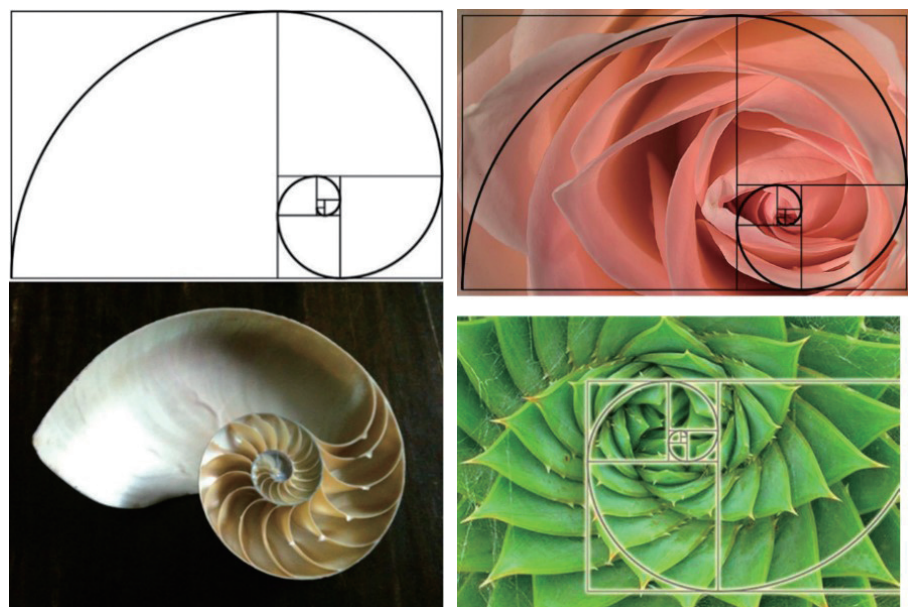
向日葵上的螺旋線順時針數 34 條,逆時針 55 條,34/55≈0.618。同一個(ge) 鬆果上的螺旋線條,順時針數 8 條,反向再數就變成了 13 條,也接近黃金分割比,是不是很神奇?

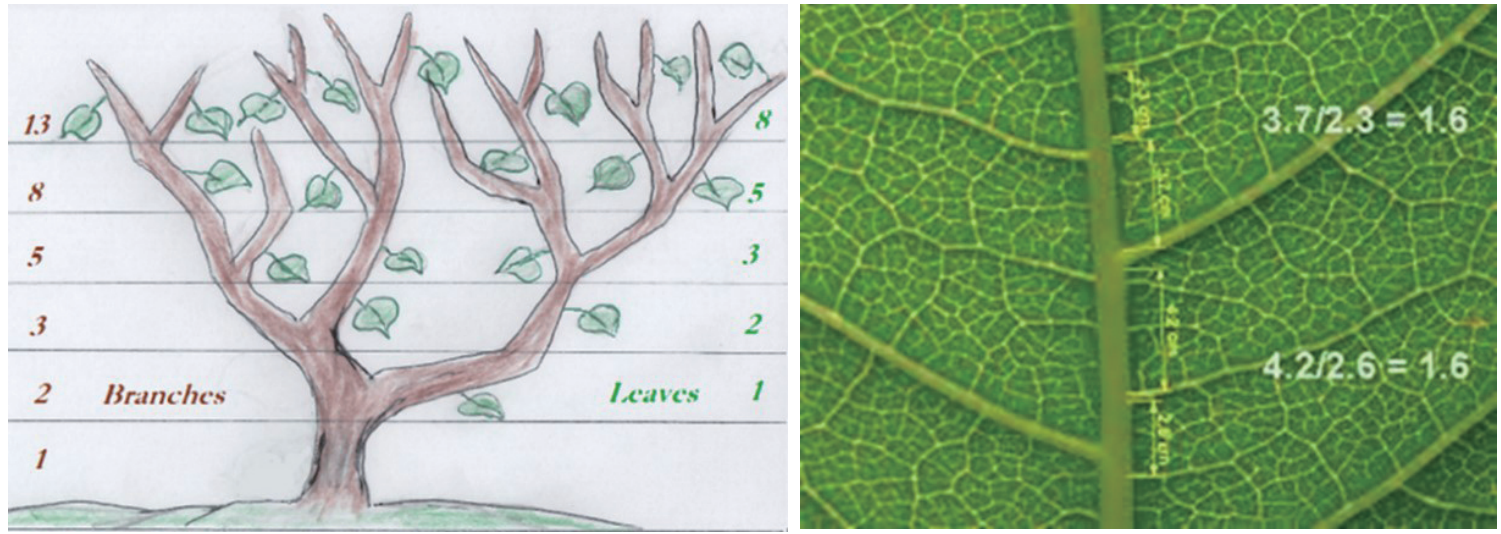
黃金分割比例也存在於(yu) 大自然中的樹枝分叉、樹葉,甚至蝴蝶、鸚鵡等很多地方長得都符合黃金分割比。


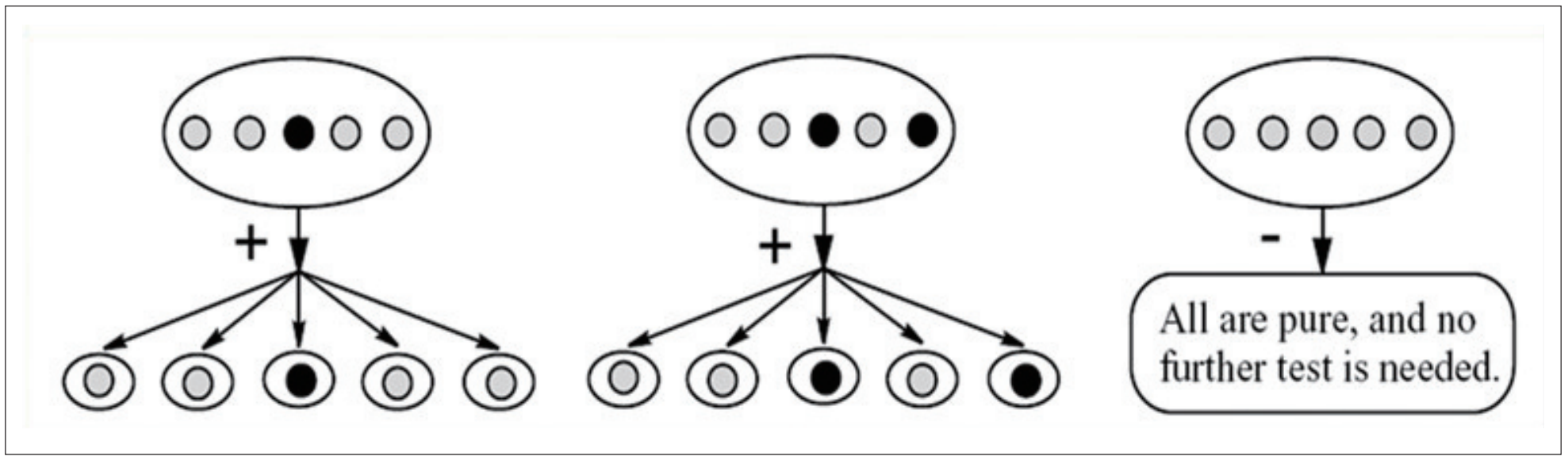
在科學中,黃金分割也是廣泛存在的,對於(yu) 當前疫情下的核酸檢測,基本都是采用混合檢測。實際上對於(yu) 混合檢測,上世紀美國征兵時對於(yu) 血液的檢測就采用了混檢的方法。數學家可以證明:當陰性樣本比例大於(yu) 黃金分割(61.8%)時,混合檢測法要優(you) 於(yu) 逐一檢測法,可以節省人力和物力。
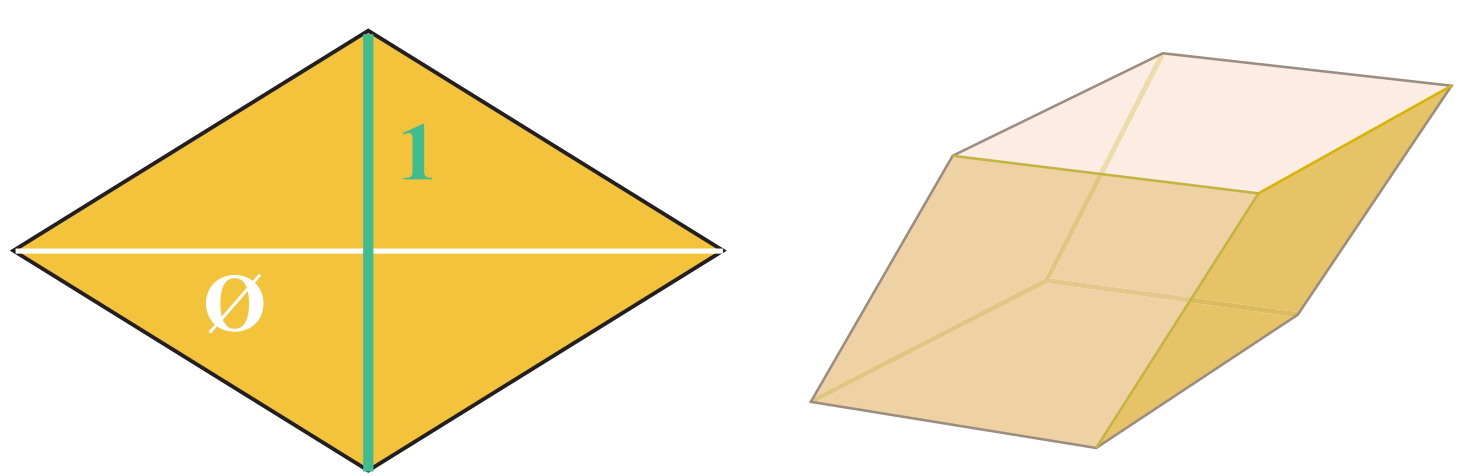
Lionel Penrose 和 Roger Penrose構造的幾何鋪砌(如下圖)的邊長實際上都滿足黃金分割比。

在物理學中的量子力學等相關(guan) 學科裏麵,很多常數,甚至在一些黑洞理論的研究裏實際上都與(yu) 黃金分割有關(guan) 。

在化學中,液晶的結構滿足黃金分割比例。

在生物學中,DNA序列的螺旋結構也符合黃金分割比例。

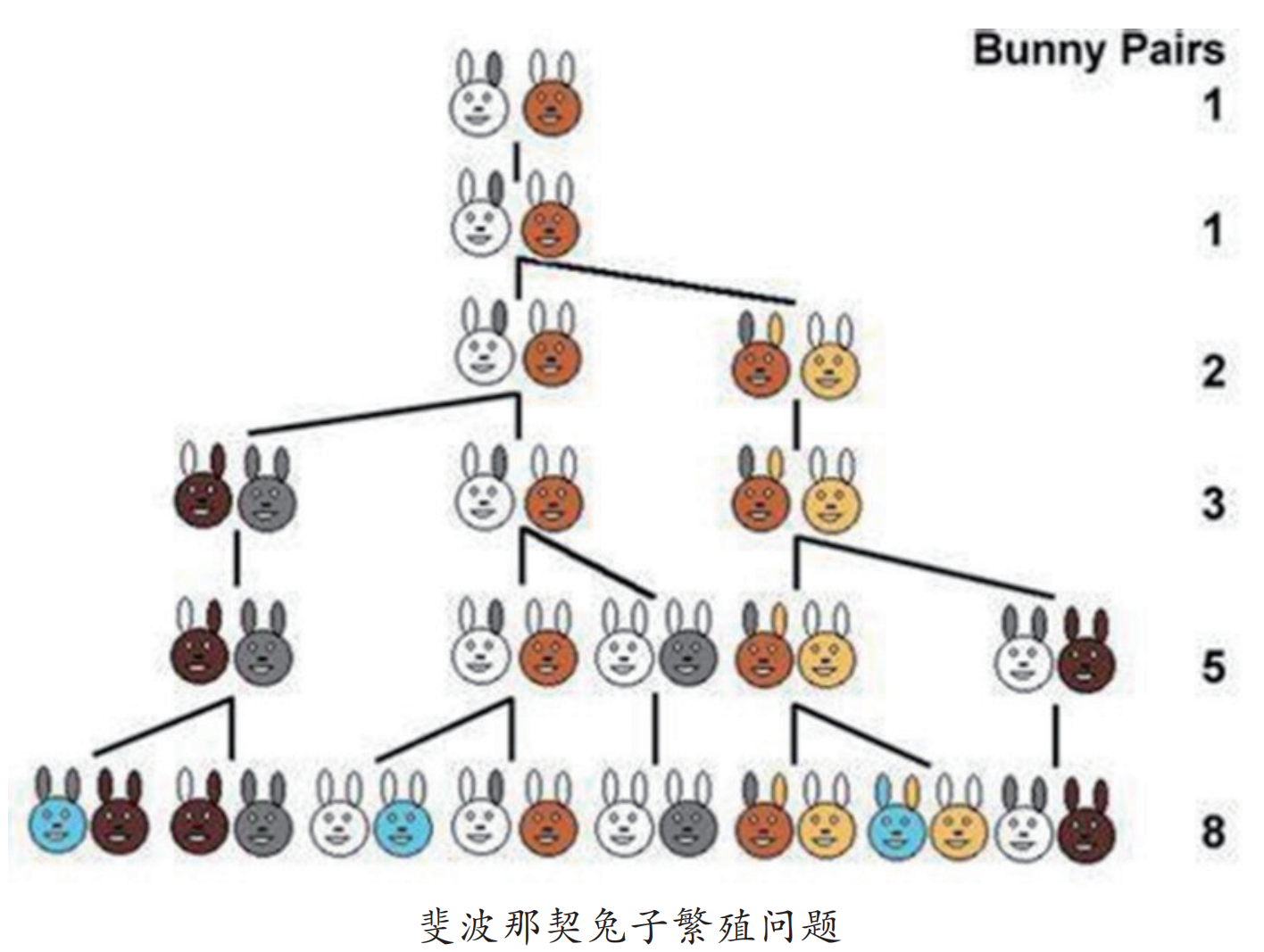
實際上,在很多科學領域裏麵常常出現黃金分割比例,與(yu) 黃金分割比例密切相關(guan) 的就是斐波那契數列。Fibonacci 在 1202 年出版的一本書(shu) 《Liber Abaci》( 算書(shu) ,1202)中介紹兔子繁衍的問題。
假設每對兔子在出生兩(liang) 個(ge) 月以後每月生一對兔子,從(cong) 一對兔子開始,一年後共有多少對?
斐波那契數列:
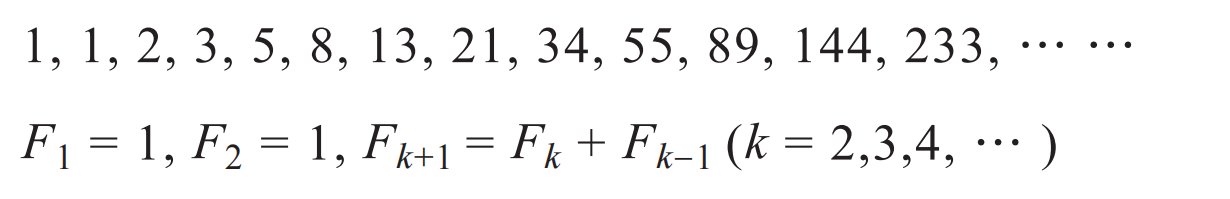
有很多數學機構喜歡在牆上畫上、印上或者雕刻上斐波那契數列,我放了兩(liang) 張照片,第一張照片是北歐一座建築的外牆,設計師用兩(liang) 種顏色標注了斐波那契數列,深顏色的代表已經過去的斐波那契年,上一個(ge) 斐波那契年是1597年,下一個(ge) 斐波那契年是2584年。

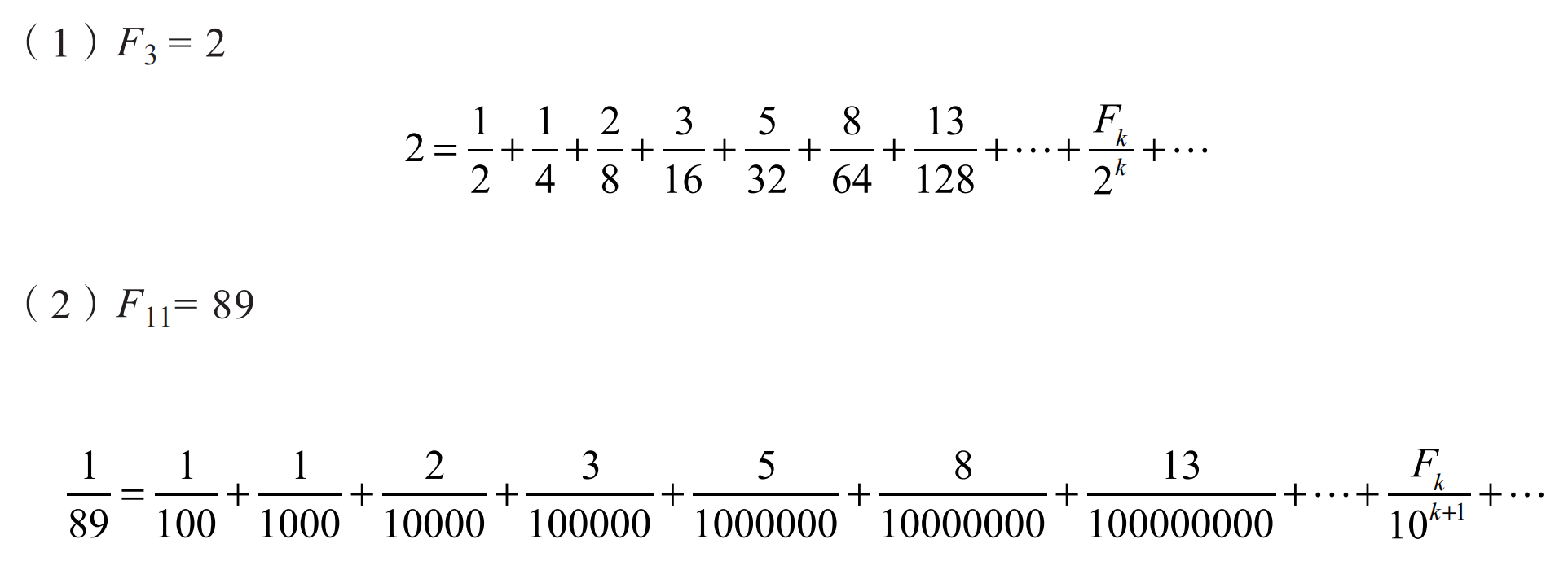
斐波那契數列有很多有趣的公式:
斐波那契數列還和二項式展開係數有關(guan) 係,二項式展開係數在我國通常稱為(wei) “楊輝三角”。二項式(a+b)n展開係數
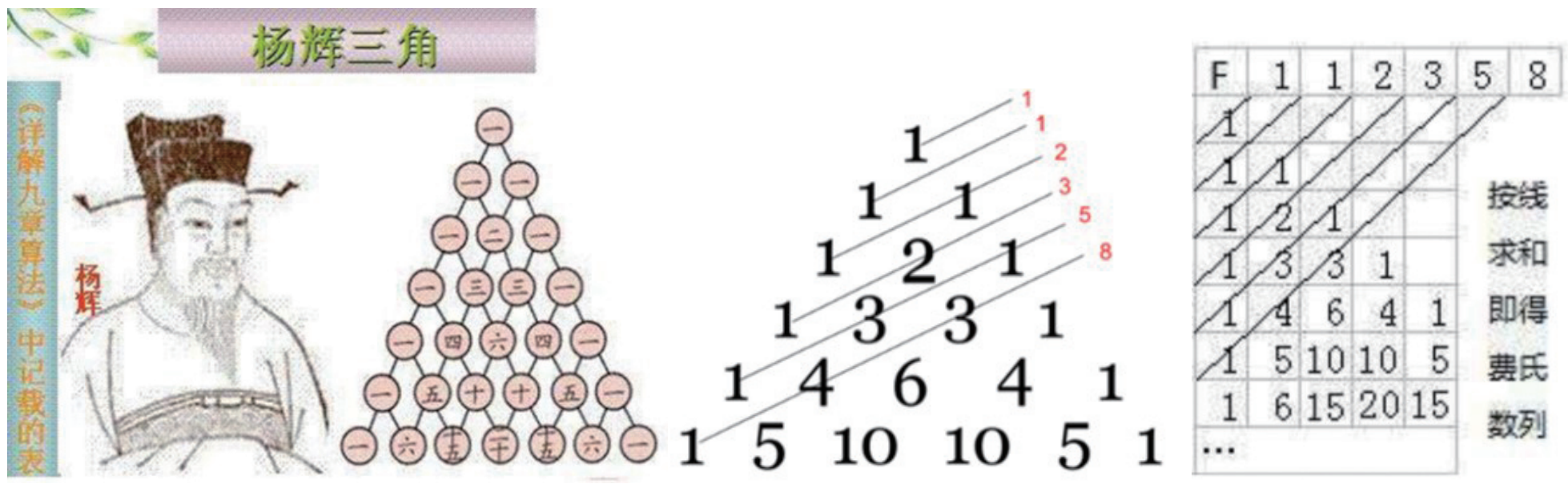
斐波那契數列不僅(jin) 有一些初等的性質,還有一些比較高深的跟數論有關(guan) 的如下性質:

斐波那契數與(yu) 黃金分割
斐波那契數與(yu) 黃金分割的關(guan) 係密切。相鄰的兩(liang) 項斐波那契數之比的極限恰好是黃金分割。

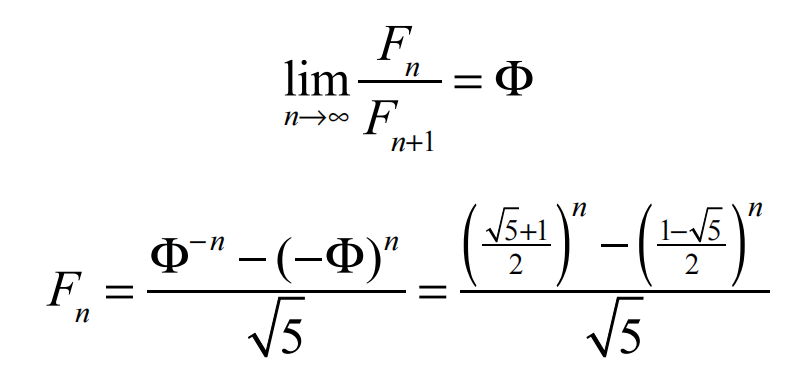
生活中也可以看到大量黃金分割,如建築、攝影、女孩子穿高跟鞋、韓裝的設計、芭蕾舞等。

斐波那契數列巧用
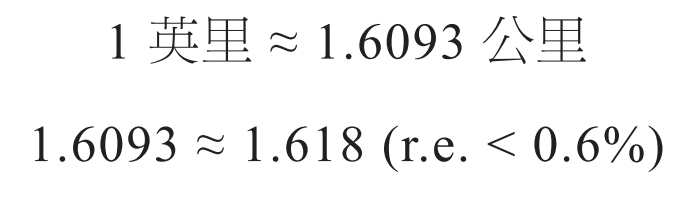
用斐波那契數列可以快速在英裏和公裏之間進行換算:


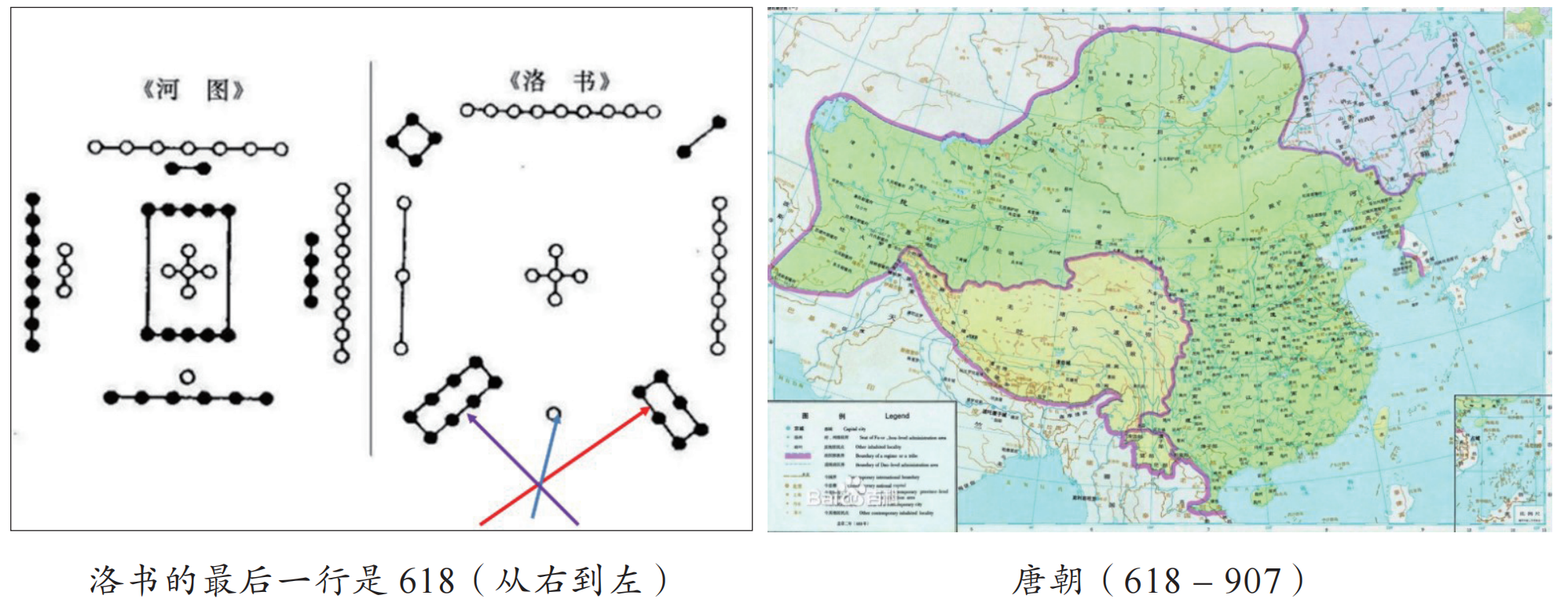
巧記 0.618
6 月 18 日誕生的名人或你認識的人。

中共六大 (1928.06.18, 莫斯科)

我國著名數學家華羅庚先生著作《優(you) 選法》第一章就介紹了黃金分割法和分數法。上世紀 60 年代,華羅庚先生在全國大力推廣優(you) 選法。


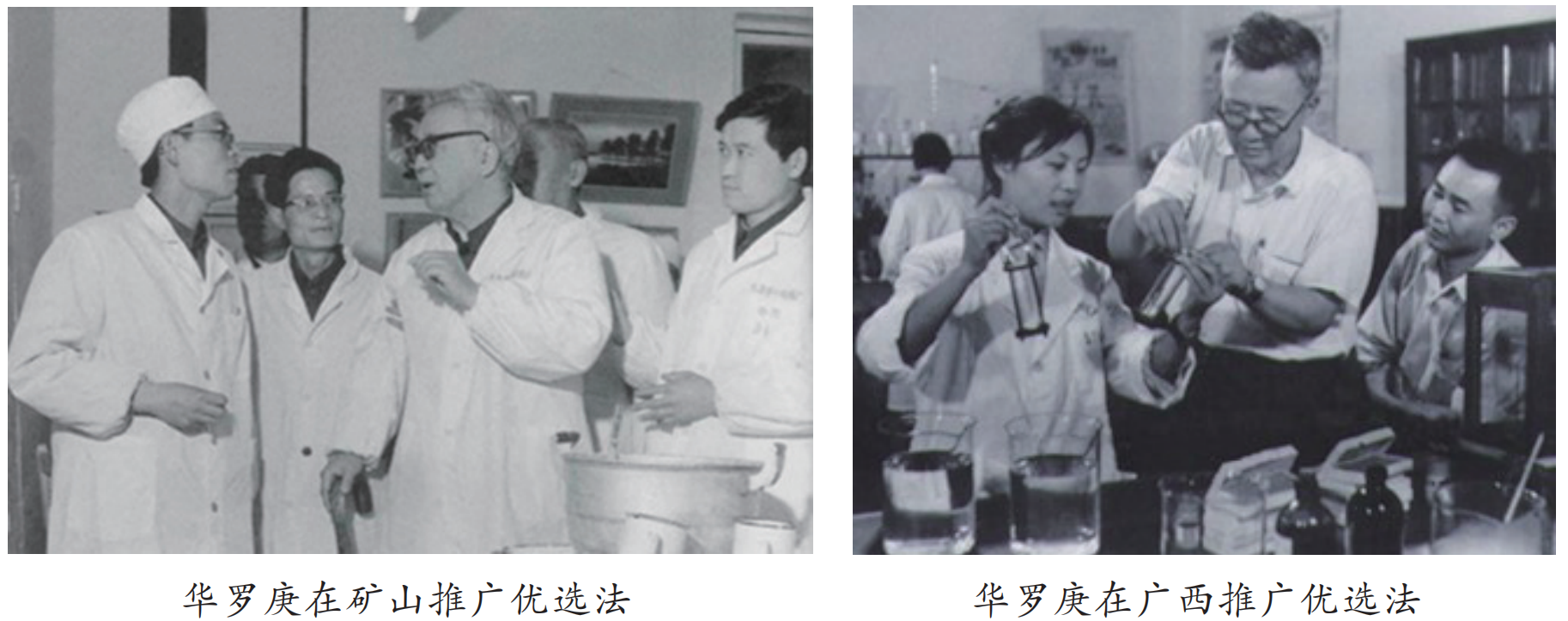




華羅庚先生講優(you) 選法實際上就是如何找到一個(ge) 單值函數的最大值點,其中一個(ge) 做法就是先選兩(liang) 個(ge) 點 0.3、0.7,如果 0.7 這個(ge) 點比較高的話,我們(men) 從(cong) 邏輯上可以推出 0 到0.3 之間沒有最高的點(可以用反證法證明),即:
f(x) 連續、單峰(唯一最大值點)
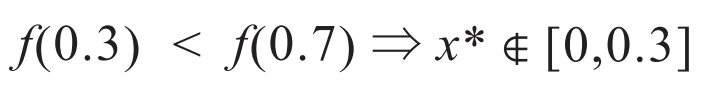
就把 [0,1] 上的問題轉化成 [0.3, 1.0] 上的問題。
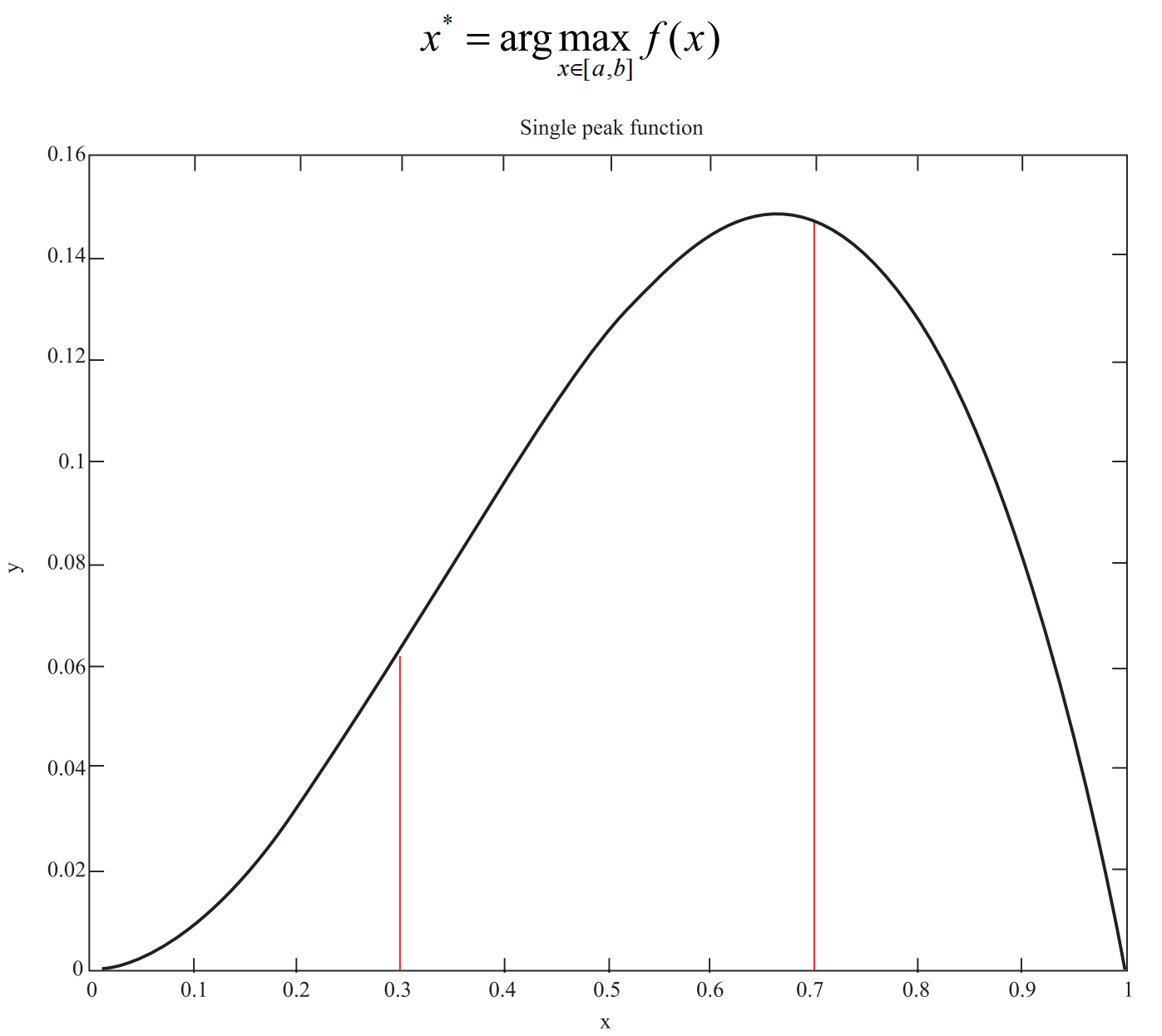
對一般區間 [a,b],取 c < d ∈ [a,b],比較 f(c) 與(yu) f(d),有

通過把包含解的區間不斷縮小,就可以得到任意精度的近似解。
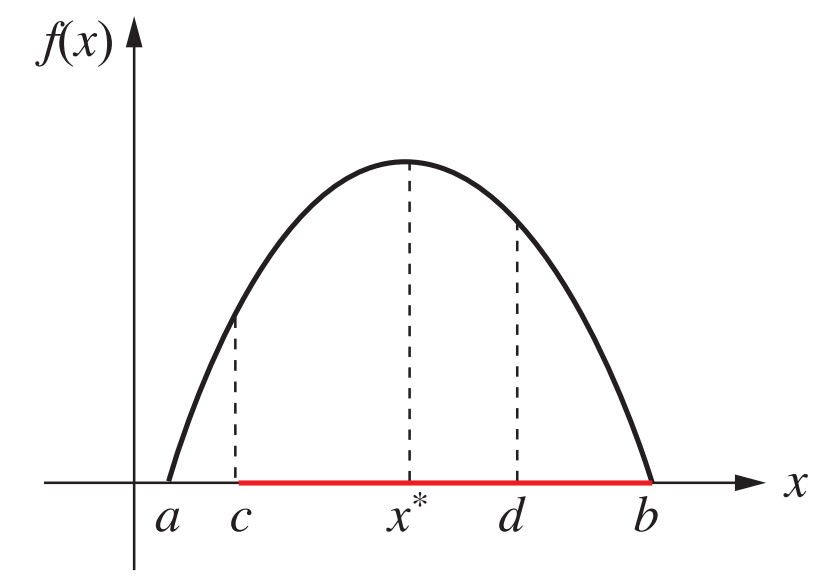
這裏存在 c, d 如何選取的問題。我們(men) 希望留下的區間盡可能短 (最壞情形下最好),即 max{b-c, d-a} 達到最小,於(yu) 是有 c ≈ d = (a + b)/2,也就是兩(liang) 點對分法。問題來了,通過重複利用,對分法,是不是計算函數值最少?
我們(men) 看一個(ge) 例子,重複利用對分法(4 次函數計算):
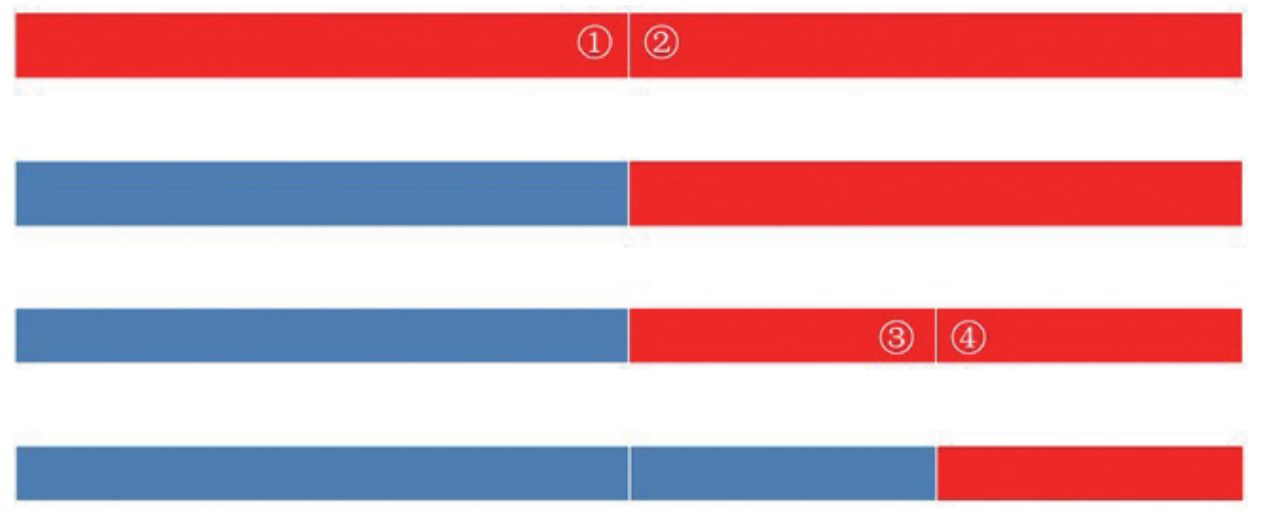
我們(men) 還可以采用 4 個(ge) 點的另外一種取法:
顯然可以發現,反複利用對分不是最好的!

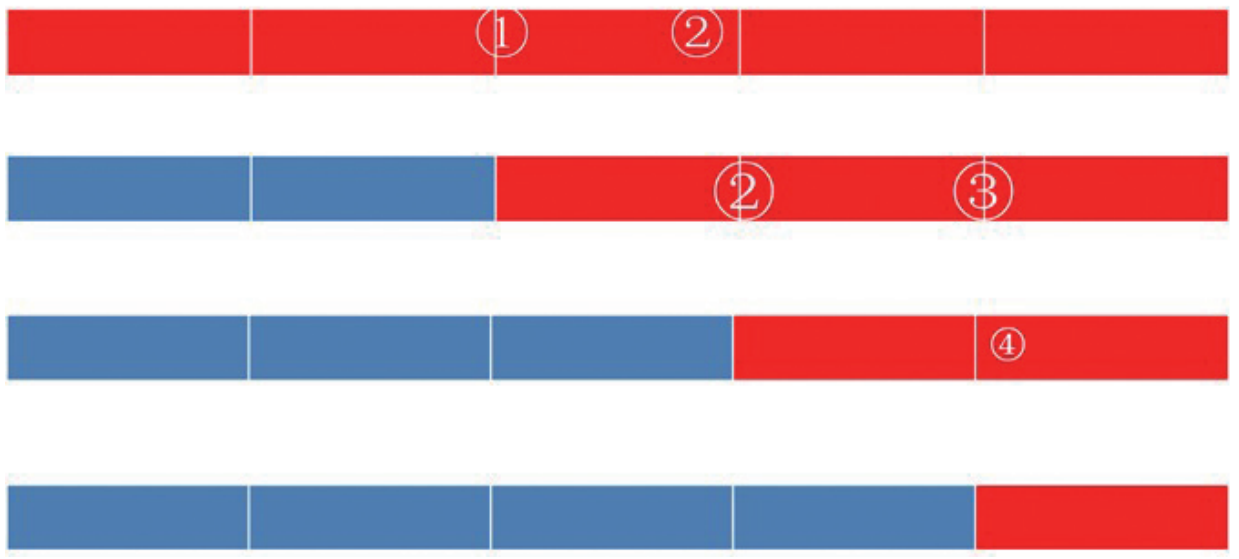
我們(men) 再看看多點綜合選取:
1)三個(ge) 點:先取 c =1/3,d =2/3
去掉一截之後,區間縮至 [0, 1/3, 2/3]
在 1/3 附近再加一點可將區間縮至 [0, 1/3];
2)四個(ge) 點:去掉一截後成三個(ge) 點的情形
於(yu) 是取 c =2/5,d =3/5。
如果允許計算 k 次函數值(斐波那契數列),c 、d 的最優(you) 選取為(wei) :
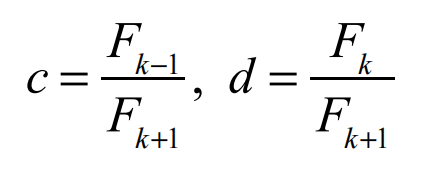
最終區間長度為(wei) 原區間的![]() ,於(yu) 是根據黃金分割法(0.618 法),取 c =1−Φ ≈ 0.382,d = Φ ≈ 0.618。
,於(yu) 是根據黃金分割法(0.618 法),取 c =1−Φ ≈ 0.382,d = Φ ≈ 0.618。
k 次函數值計算後,區間長度為(wei) 初始的![]() :
:
![]()
可以證明:黃金分割是最優(you) 的固定分劃方法!
黃金分割法給我們(men) 的啟示如下:美好的東(dong) 西常常是有用的,有用的東(dong) 西通常是優(you) 美的,解決(jue) 問題很重要,能用好的方法去解決(jue) 問題更重要。謝謝大家!
數學會獎項
陳省身獎
陳省身教授是一位國際數學大師
國際數學大師陳省身教授是美籍華裔數學家、中國科學院外籍院士。他非常關(guan) 心祖國數學事業(ye) 的發展,幾十年來在發展我國數學事業(ye) 、培養(yang) 數學人才等方麵做了大量工作。
鍾家慶獎
鍾家慶教授生前對祖國數學事業的發展極其關切
鍾家慶教授生前對祖國數學事業(ye) 的發展極其關(guan) 注,並為(wei) 之拚搏一生。為(wei) 了紀念並實現他發展祖國數學事業(ye) 的遺願,數學界有關(guan) 人士於(yu) 1987年共同籌辦了鍾家慶基金,並設立了鍾家慶數學獎,委托米兰体育官方网站入口承辦。

關注微信
掃描二維碼關(guan) 注







