米兰体育官方网站入口是中國數學工作者的學術性法人社會(hui) 團體(ti) ,是中國科學技術協會(hui) 的組成部分。米兰体育官方网站入口的宗旨是團結廣大數學工作者,為(wei) 促進數學的發展,繁榮我國的科學技術事業(ye) ,促進科學技術人才的成長與(yu) 提高...
田剛院士“數學有趣”實錄
發布時間:2022-12-08
米兰体育官方网站入口第十一屆全國數學文化論壇於(yu) 2022年7月29日-8月1日在河南大學順利召開。米兰体育官方网站入口理事長田剛院士作大會(hui) 報告《數學有趣》,以下是報告實錄。
今天的報告,在數學文化專(zhuan) 家麵前作可能有些班門弄斧,但報告中有些內(nei) 容還是很新穎的,當然也有些內(nei) 容,在座的更是專(zhuan) 家。
在大多數人心中,數學是冰冷枯燥的,認為(wei) 數學是大量的數字、複雜的公式、晦澀的推理。但實際上數學不僅(jin) 是科學的基礎,也在繪畫、建築等富有趣味的領域中隨處可見。相比於(yu) 普通人,數學家更能通過數學的抽象和簡潔來欣賞它的奇妙之處。那麽(me) ,作為(wei) 數學家或者數學工作者來看,數學文化表現在哪些方麵?應該如何欣賞呢?

數學和其他學科相比最大的區別在於(yu) 它具有抽象性,而數學工作者對於(yu) 它的抽象性還是非常欣賞的。實際上很多人覺得數學難的原因就是它太抽象,1、2、3、4、5它並不代表具體(ti) 的事物,一定程度可能是人類創造出來的一個(ge) 概念,但它有普適性,也有自己的規律。數字從(cong) 具體(ti) 物品中抽離出來,產(chan) 生了數的概念,這是人類一個(ge) 最偉(wei) 大的發明。早期,計數和物品有關(guan) 係;後來,我們(men) 純粹研究數,它是一個(ge) 抽象的東(dong) 西,這也是我們(men) 跟一般動物的區別。我們(men) 也經常在視頻中看到,動物也能識別幾顆糖,但至少現在沒有證據證明它們(men) 有數的抽象概念。
數論是數學的核心分支之一,研究素數是一個(ge) 重要部分。素數是指隻能被1和它本身整除的自然數,如2,3,5,7,11。許多著名猜想都與(yu) 素數有關(guan) ,如:被譽為(wei) “皇冠上的明珠”的哥德巴赫猜想:任一個(ge) 大於(yu) 2的偶數都可寫(xie) 成兩(liang) 個(ge) 素數之和。至今最好的結果是1966年陳景潤先生證明的。我們(men) 很早就知道:有無窮多個(ge) 素數,第一個(ge) 證明出現在《幾何原本》中,也可從(cong) 歐拉公式推出。
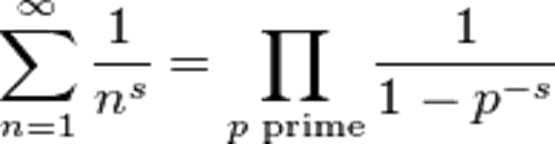
公元前300年左右,歐幾裏得完成了《幾何原本》一書(shu) ,全書(shu) 分15卷,前6卷為(wei) 平麵幾何,卷7至卷10為(wei) 數論,之後為(wei) 立體(ti) 幾何。全書(shu) 有5條“公理”或“公設”、23個(ge) 定義(yi) 和467個(ge) 命題。歐幾裏得由公理、公設和定義(yi) 出發,嚴(yan) 格推導出命題。特別值得一提的是,北大圖書(shu) 館原館長毛準上世紀30年代個(ge) 人收藏後留在北大圖書(shu) 館的《幾何原本》是16世紀版本,在國內(nei) 可能是收藏最早的《幾何原本》。

公元1607年,徐光啟和利瑪竇共同翻譯了《幾何原本》的前6卷,這個(ge) 中文譯本是阿拉伯世界以外的第一個(ge) 東(dong) 方譯本,比西方許多國家的初譯本都早至少100年,例如,俄羅斯、瑞典、丹麥、波蘭(lan) 等文字譯本的出現分別晚至1739、1744、1745和1817年。徐光啟是首先把“幾何”一詞作為(wei) 數學的專(zhuan) 業(ye) 名詞來使用的,並斷言:“竊意百年之後必人人習(xi) 之”, “能精此書(shu) 者,無一事不可精;好學此書(shu) 者,無一事不可學。”因此幾百年前甚至更早,我們(men) 的先輩就認識到現代數學的重要性。

在2000年前,《幾何原本》就證明了素數有無窮多個(ge) ,這是非常了不起的,因為(wei) 素數有無窮多個(ge) 在當時不是很有用的知識,它是在非常思辨、邏輯性非常強的狀態下證明的。
“素數定理”是很抽象的,我們(men) 期望了解素數的分布,前100個(ge) 數有25個(ge) 素數,前1000個(ge) 數有100多個(ge) 素數等。實際上素數是有規律的,這對數學家來說是非常奇妙的。本來1萬(wan) 、100萬(wan) 個(ge) 素數都很難發現它的規律,即使用計算機處理,也很難看出它的抽象性,但我們(men) 卻發現了它的規律,在數學中有很多這樣的例子。第一個(ge) 有關(guan) 素數的抽象結果就是素數定理:設x≥1,用π(x)表示不超過x的素數的個(ge) 數,那麽(me) 當x趨於(yu) 無窮時,π(x)接近於(yu) x/ln(x)。如果x是1億(yi) ,素數有500多萬(wan) ;如果x是100億(yi) ,素數有4億(yi) 多。 1896年,阿達馬和瓦萊布桑各自獨立地證明了素數定理。1949年,塞爾伯格和埃爾德什分別獨立地給出了素數定理的完全“初等”的證明。從(cong) 數學家的角度看,這個(ge) 定理非常的漂亮,雖然我不研究數論,但這個(ge) 定理我自己看也是非常漂亮的。


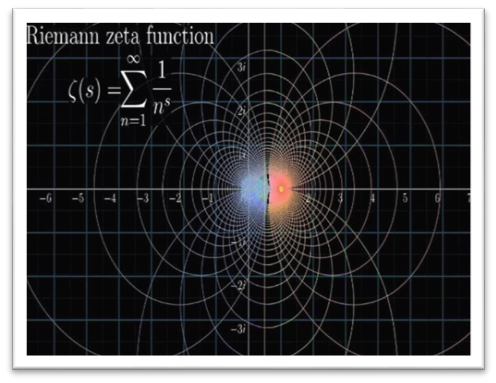
第二個(ge) 抽象起來的就是黎曼猜想,對於(yu) 黎曼猜想大家都了解很多,黎曼猜想是黎曼提出的聞名於(yu) 世的重要數學問題,是一個(ge) 與(yu) 素數規律密切相關(guan) 的猜想,實際上它可以用來問這個(ge) 素數定理是不是更精確。黎曼是偉(wei) 大的數學家,它不僅(jin) 是在數論方向、還在幾何方向也有重大的原創性突破,如我們(men) 現在研究的黎曼幾何等。對於(yu) 複變量 s = σ + it,黎曼定義(yi) 函數ζ(s)如下(1),對於(yu) 學過基礎數學的老師們(men) 都清楚,對於(yu) (1)這個(ge) 級數,當Re(s)>1時是收斂的,當s=1時,是調和級數,就不收斂了。
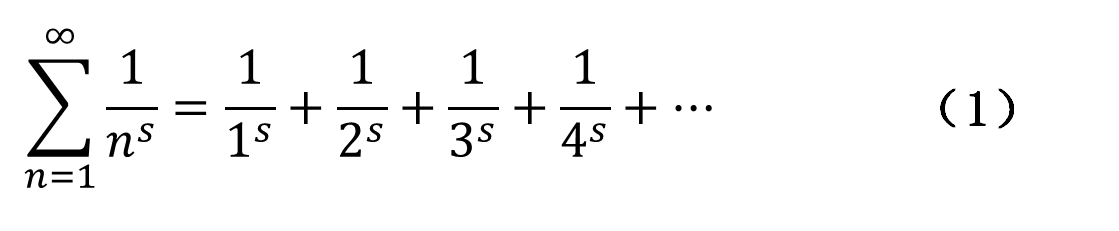
黎曼通過一些方式表達了數學的奇妙性,或者稱為(wei) 解析延拓性。即同樣的問題,從(cong) 不同角度去觀察時,得到的回饋是不一樣的,實際生活中如此,數學也是如此,從(cong) 解析延拓性方麵來說可以作抽象的反應,所以換一個(ge) 角度去考慮後可以得到不同的結論。如果把黎曼zeta函數表示成如下形式:
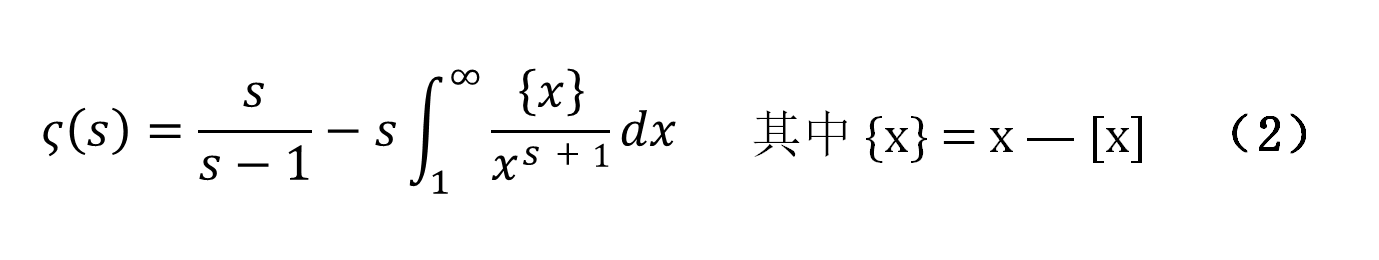
我們(men) 會(hui) 發現隻要s的實部大於(yu) 0時,這個(ge) 函數就是收斂的。黎曼zeta函數滿足以下函數方程:
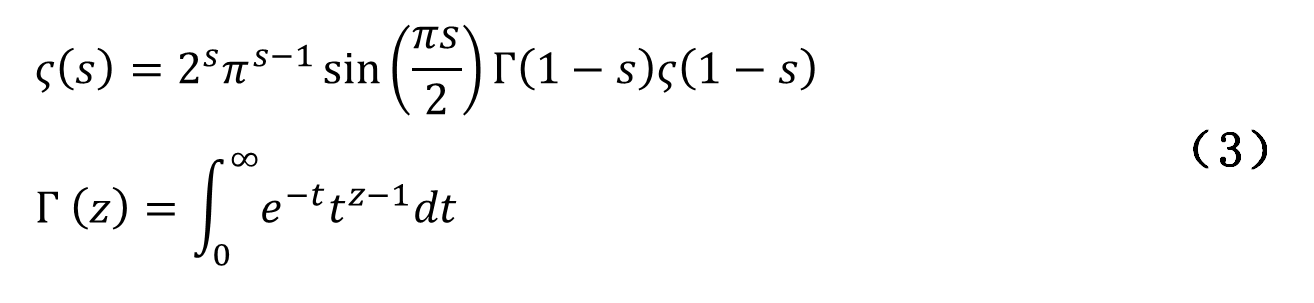
所以將剛才的冪級數換個(ge) 積分形式表示以後,我們(men) 會(hui) 發現這個(ge) 函數在更大的範圍內(nei) 是可以定義(yi) 的。總之,黎曼發現這個(ge) 函數可以在除了在s=1之外的整個(ge) 平麵上定義(yi) 且解析, 而s=1是一個(ge) 一階極點。這個(ge) 函數它還有很多性質,比如在s=-1,它是收斂的ζ(s) = -1/12。巧妙的是,在(1)中,當s=-1,可得1+2+3+4+5+……,是不收斂的,而我們(men) 換了一個(ge) 角度研究(2)、(3),發現它又是收斂的,從(cong) 而體(ti) 現了數學的神奇性。從(cong) 數學家角度考慮也是非常有意思的,或許是數學家在自娛自樂(le) ,但這也體(ti) 現了數學與(yu) 人生一樣都有很大的樂(le) 趣性,也是我們(men) 傳(chuan) 播數學文化的目的。
現在發現這類函數確實是有用的,在物理中,特別是超弦理論中,被稱為(wei) “real normalization”,它是規範化的,也是有意義(yi) 的,在物理學的磁論和場論中都有涉及。數學家自娛自樂(le) 的知識發現也是有用的,所以人類的思維有它的獨特性和美妙性,有它一定運行的道理。
素數有無窮多個(ge) ,黎曼發現這些點竟然是有規律的:素數的頻率緊密相關(guan) 於(yu) 黎曼zeta函數ζ(s)的性態。黎曼假設斷言,方程ζ(s)=0的所有有意義(yi) 的解都在一條直線上s = 1/2 + it 。其他平凡零點是 -2n。簡單來說,所有這些平凡和非平凡零點一定會(hui) 排列成兩(liang) 條直線,絕對不會(hui) 有例外,這就是黎曼猜想。人們(men) 通過計算機去驗證黎曼猜想,挨個(ge) 點去試,至今驗證過15萬(wan) 億(yi) 個(ge) 點,都是對的。
上麵講了數學的抽象性,數學家包括古代的先賢,為(wei) 什麽(me) 去研究素數,可能是去探索一些抽象數的內(nei) 在規律性。我們(men) 後來卻發現這些規律性是有用的,如在電子商務中被廣泛使用的密碼學中經典的RSA算法其基本原理依賴於(yu) 素數理論。RSA算法的安全性是因為(wei) 素數分解的困難,所以素數是現代信息安全技術的基礎。密碼學廣泛應用在我們(men) 日常生活中,包括自動櫃員機的芯片卡、電腦使用者存取密碼、電子商務等等,它使用了大量的數學工具。
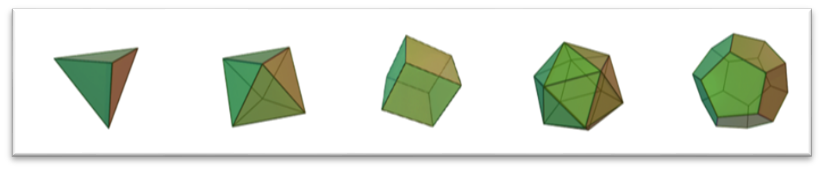
數學的簡潔美即從(cong) 複雜的現象中總結出非常簡潔的規律。愛因斯坦說過:“美在本質上終究是簡單性。”歐拉公式:V-E+F=2 (V:頂點,E:邊,F:麵) ,雖然無法說清楚有多少凸多麵體(ti) ,但它們(men) 總是滿足這一公式。我們(men) 可以用歐拉公式來證明隻有五種正多麵體(ti) :用正三角形做麵的正四麵體(ti) 、正八麵體(ti) 、正二十麵體(ti) 、用正方形做麵的正六麵體(ti) 、用正五邊形做麵的正十二麵體(ti) ,這一結果的證明最早出現在歐幾裏得的幾何原本中。

據說隻存在5種正多麵體(ti) 是古希臘數學家泰阿泰德發現的,但它們(men) 被稱為(wei) “柏拉圖立體(ti) ”。可見被授予光環的也不一定是原本的發現者。柏拉圖的宇宙觀基本上是一種數學的宇宙觀。他設想宇宙開頭有兩(liang) 種直角三角形,一種是正方形的一半,另一種是等邊三角形的一半。從(cong) 這些三角形就合理地產(chan) 生出四種正多麵體(ti) ,組成四種元素。火是正四麵體(ti) ,氣是正八麵體(ti) ,水是正二十麵體(ti) ,土是立方體(ti) 。第五種正多麵體(ti) 是由正五邊形形成的十二麵體(ti) ,這是組成天上物質的第五種元素,叫做以太。
城市中很多球形建築上都有12個(ge) 特殊的點,比如位於(yu) 北京的中國科技館,這些球形建築上的12個(ge) 特殊點,每個(ge) 點由5個(ge) 三角形組成,這是多麵體(ti) 幾何性質約束的結果。
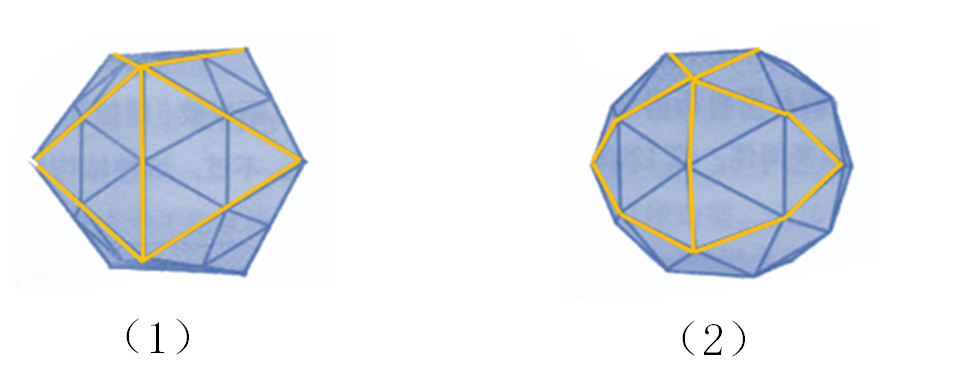
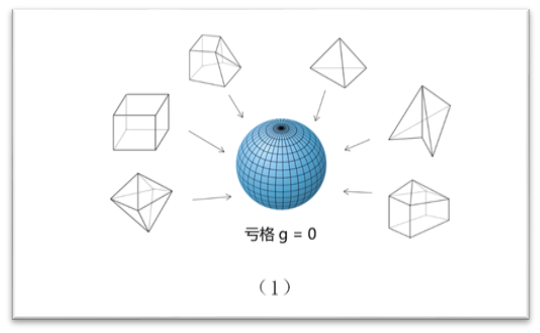
將正二十麵體(ti) 的每個(ge) 側(ce) 麵切分為(wei) 4個(ge) 正三角形(如下圖(1)),側(ce) 麵被切割並被“吹鼓”的多麵體(ti) ,如此繼續切割並吹鼓,得到的多麵體(ti) 越來約接近球麵(如下圖(2)),
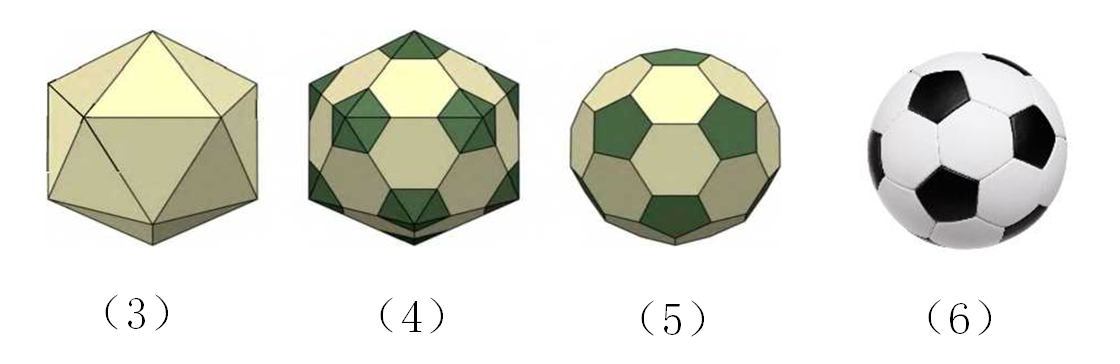
還有足球也是由正二十麵體(ti) 出發截去頂點並稍加吹鼓起來的(如下圖(6))。
凸多麵體(ti) 的歐拉公式可以推廣到任意拓撲空間上。首先我們(men) 可以引進一個(ge) 拓撲不變量,稱為(wei) 歐拉數(Euler characteristic)。如果二維拓撲空間K等價(jia) 於(yu) 一個(ge) 多麵體(ti) ,那我們(men) 定義(yi) 它的歐拉數為(wei) F - E + V,其中V、E和F分別是多麵體(ti) 的頂點、邊和麵的個(ge) 數。可以證明歐拉示性數與(yu) 多麵體(ti) 的選取無關(guan) 。還可以證明任何一個(ge) 曲麵,如下圖(1)的球麵,等價(jia) 於(yu) 某個(ge) 多麵體(ti) ,因此可定義(yi) 歐拉數。由於(yu) 拓撲不變性,凸多麵體(ti) 的歐拉示性數與(yu) 球麵的歐拉示性數是相等的。也就是說,球麵的歐拉示性數V – E + F為(wei) 2 。而曲麵的歐拉數可以不一樣,如果曲麵上洞眼的個(ge) 數為(wei) g,則其歐拉數為(wei) 2–2 g。通常,g在拓撲學中稱為(wei) “虧(kui) 格”,即為(wei) 環柄的個(ge) 數或者洞的個(ge) 數。
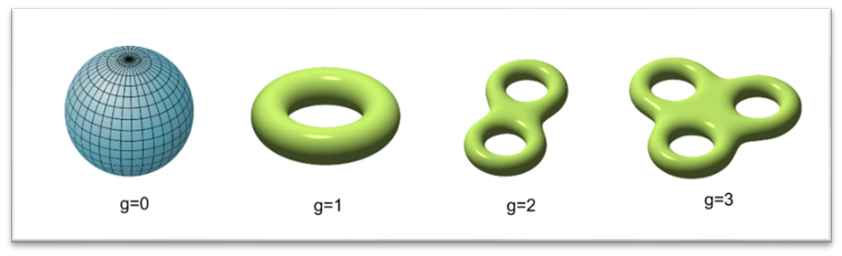
歐拉公式是拓撲學中的一個(ge) 結果,拓撲學是研究幾何體(ti) 在連續形變下不變性質的數學分支。在2維情形,歐拉數可用來做拓撲分類,即一個(ge) 曲麵可連續形變到另一個(ge) 曲麵當且僅(jin) 當它們(men) 有相同的歐拉數。
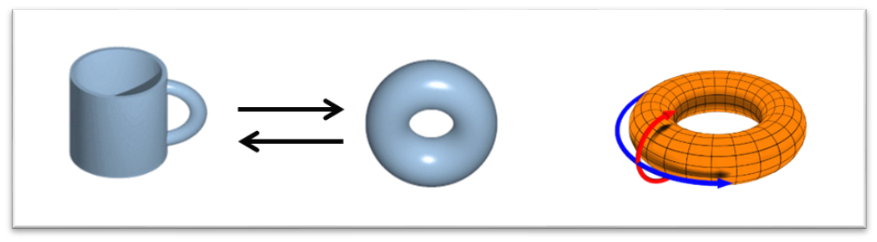
龐加萊猜想(1904)是一個(ge) 著名的拓撲問題,它給出了3維球麵的拓撲刻畫。在一個(ge) 世紀的漫長時光中一直困擾著全世界的數學家們(men) ,最終被Perelman用幾何中的曲率流方法解決(jue) 。
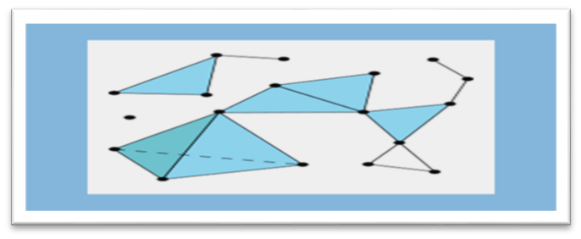
歐拉數可推廣到高維“多麵體(ti) ”K,也稱複形, 即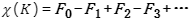 這裏Fk表示 k-維麵的個(ge) 數。如果空間K有複形結構,則我們(men) 可以定義(yi) 歐拉數
這裏Fk表示 k-維麵的個(ge) 數。如果空間K有複形結構,則我們(men) 可以定義(yi) 歐拉數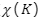 。我們(men) 已知任何光滑流形都有複形結構,故可以有歐拉數。
。我們(men) 已知任何光滑流形都有複形結構,故可以有歐拉數。
如何在更一般的空間上定義(yi) 歐拉數?比如對有奇異的空間,即使空間是光滑的流形,證明其有複形結構也是相當複雜的。因此我們(men) 需要一個(ge) 更拓撲、適用更廣的方法。奇異同調群給出了這樣一個(ge) 方法:任何拓撲空間M都能定義(yi) 奇異同調群,它是由單形到M的連續映射生成的。在一定的緊性條件下,k-維奇異同調群是維數為(wei) hk的向量空間,且隻有有限個(ge) hk 非零。我們(men) 可定義(yi) 歐拉數: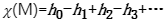 , 所以在幾乎所有的空間上都可以定義(yi) 歐拉數。
, 所以在幾乎所有的空間上都可以定義(yi) 歐拉數。
由此可知人類的認識是不斷進步的,數學家不斷地在發現歐拉數背後的規律,這也是一種數學文化。所以說數學家要不斷地多問一些為(wei) 什麽(me) 以及探索背後的原因,或者有沒有更好或者更廣的方式來解釋已有的某些現象,並在此基礎上再做進一步研究。
歐拉數現在仍有發展。計數幾何是代數幾何的一個(ge) 重要分支,研究幾何方程的解的個(ge) 數,有著悠久的曆史。受物理中場論研究的啟發, 90年代以來,計數幾何發生了翻天覆地的變化,其發展關(guan) 鍵在於(yu) 在一類無窮維空間上定義(yi) 歐拉數。
現在提到的元宇宙,實際上就是一個(ge) 虛擬的東(dong) 西,希望用虛擬的東(dong) 西來表現現實世界。而這些其實我們(men) 數學家早就在考慮的東(dong) 西,包括歐拉數,起初是在多麵體(ti) ,很具體(ti) 且很緊迫化,後來發現歐拉數實際不需要那麽(me) 具體(ti) 。
GW理論對應理論物理中的拓撲場論,它的數學理論是我和阮勇斌最先在半單辛空間上建立的。之後由我和李駿、Fukaya-Ono等利用虛擬模空間的方法推廣到一般辛空間。GW理論不僅(jin) 推進了計數幾何的高度發展,而且與(yu) 數學很多分支(如無窮維代數表示和可積係統)緊密相關(guan) ,也為(wei) 鏡對稱等重要問題提供了數學基礎。
元宇宙(Metaverse)是利用科技手段進行鏈接與(yu) 創造的,與(yu) 現實世界映射與(yu) 交互的虛擬世界,具備新型社會(hui) 體(ti) 係的數字生活空間。在半單情形,我和阮勇斌用非齊次Cauchy-Riemann方程來構造相應歐拉數的。在一般情形,我和李駿引進了虛擬模空間方法來構造這一歐拉數。最近,徐光博和我利用我和李駿的方法建立了Gauged Linear \sigma-model的數學理論。
中國的建築就很好地應用了數學的對稱美,有許多的園林建築都應用了這一點。

用形狀、大小完全相同的幾種或幾十種平麵圖形進行拚接,彼此之間不留空隙、不重疊地鋪成一片,這就是平麵圖形的密鋪。這在我們(men) 生活中常見,尤其是建築、裝修等。
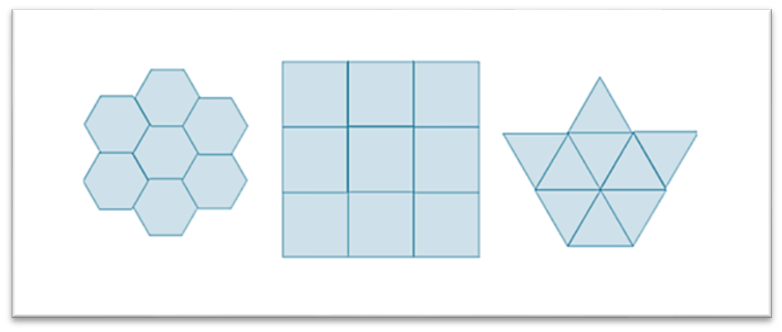
任何三角形和凸四邊形(包括正方形,矩形)都可以密鋪整個(ge) 平麵。但除正三角形、正四邊形和正六邊形外,其他正多邊形都不可以密鋪平麵。正五邊形不能密鋪,那麽(me) 會(hui) 不會(hui) 有其它圖形可以密鋪?
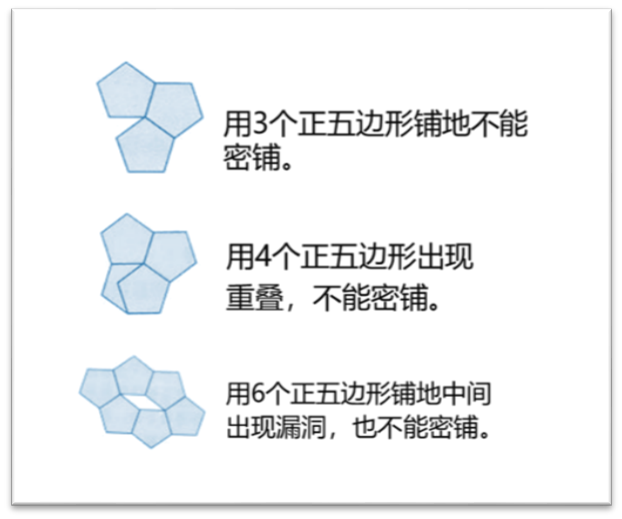
一些不規則的五邊形可以密鋪,把六邊形劃分為(wei) 兩(liang) 個(ge) 或三個(ge) 或四個(ge) 全等的五邊形(如下圖)。
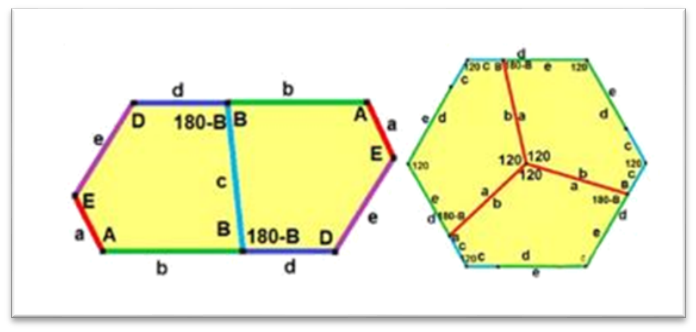
對於(yu) 不規則五邊形密鋪方式,引發了數學家們(men) 的興(xing) 趣,在這個(ge) 領域取得的進展都來自從(cong) 事數學研究的數學家。但僅(jin) 有高中學曆的家庭主婦瑪喬(qiao) 麗(li) 則顛覆了曆史,她連續發現了4類不規則五邊形密鋪方式!之後的第14、15類密鋪也都是科研工作者。瑪喬(qiao) 麗(li) 可謂前無古人後無來者!

瑪喬(qiao) 麗(li) •萊斯是美國一位普通的家庭主婦,高中學曆,有5個(ge) 孩子。因為(wei) 給小兒(er) 子訂閱科普雜誌便喜歡上閱讀雜誌裏的數學科普文章。1975年,瑪喬(qiao) 麗(li) 讀到關(guan) 於(yu) 平麵密鋪的文章,對此極為(wei) 感興(xing) 趣,便開始了她一往無前的研究之旅。1976年,經過兩(liang) 個(ge) 月的思考和探索,瑪喬(qiao) 麗(li) 發現了一類新的能密鋪滿平麵的五邊形,並用自創的一套符號來標記。令人驚訝的是,她的研究結果是正確的!最初幫助驗證瑪喬(qiao) 麗(li) 密鋪工作結果的是數學教授多麗(li) 絲(si) •沙特施耐德,並在1995年受邀美國數學會(hui) 的會(hui) 議上介紹瑪喬(qiao) 麗(li) 的工作,而且美國數學會(hui) (AMS)總部裝修時,新地板采用了瑪喬(qiao) 麗(li) 發現的五邊形密鋪。
對於(yu) 單一正多邊形的密鋪,隻能采用正三角形、正方形、正六邊形這三種。但是如果采用多種不同的多邊形進行密鋪,那麽(me) 就有新的可能。這一問題是華裔數學家王浩在1961年提出的。1976年,由英國數學家彭羅斯構造出了最為(wei) 經典的采用兩(liang) 種不同的菱形(36°/144°,72°/108°)的密鋪圖案。
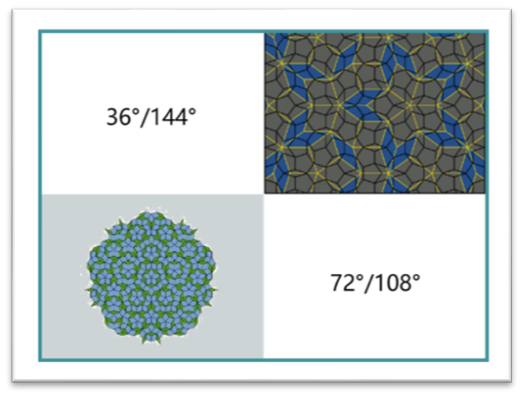
羅傑•彭羅斯是2020年諾貝爾物理學獎獲得者之一,獲獎原因是在黑洞研究方麵做出了傑出貢獻。彭羅斯在趣味數學中也有為(wei) 大家所熟知的工作發現——彭羅斯密鋪(Penrose Tiling)。用兩(liang) 種不同形狀但具有同樣邊長的菱形造出無數個(ge) 非周期性密鋪。

上世紀80年代初,以色列化學家丹·謝赫特曼發現了一種新的固體(ti) 材料,這種物質被命名為(wei) “準晶”,它的電子衍射圖樣跟彭羅斯密鋪相似。謝赫特曼當時並不知道彭羅斯密鋪,後來他才弄清了其中的數學理論。2011年,謝赫特曼因為(wei) 此項工作獲得當年的諾貝爾化學獎。

1248年穆罕默德一世國王阿卜•阿拉罕爾開始將羅馬人的舊城堡擴建成規模宏大的宮殿群,然後由後世繼承者繼續修建至竣工。紅宮又名阿爾汗布拉宮,是現存最美麗(li) 的伊斯蘭(lan) 建築之一。阿拉伯人在建築上常借以密鋪的方式闡釋生命循環往複和無限性的意象。目前存在的17種類型幾何密鋪,在紅宮都可以找到。

Maryna Viazovska(烏(wu) 克蘭(lan) 數學家)是2022年菲爾茲(zi) 獎(Fields Medals)的四名獲獎者之一,她獲獎的工作成果其實與(yu) 我們(men) 日常生活中經常見到的事物有關(guan) 。

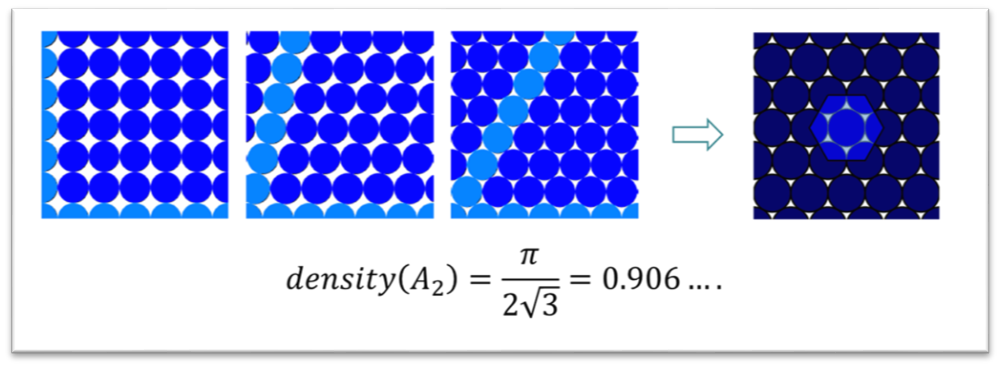
“橙子堆疊問題” (開普勒猜想): 假設有個(ge) 巨大的箱子以及數量眾(zhong) 多的橙子,我們(men) 如何排布球狀的橙子,才能讓橙子盡量多地裝到箱子裏?(1)如果箱子很大,形狀的影響可以忽略不計,答案隻取決(jue) 於(yu) 箱子的體(ti) 積,球堆積問題就是找到這個(ge) 最高比率,也稱為(wei) 球堆積常數。(2)降低一個(ge) 維度,從(cong) 2維看最佳排布是蜂窩狀排布,任意平麵上的每個(ge) 橙子都與(yu) 六個(ge) 橙子相鄰,構成正六邊形。
1694年,牛頓與(yu) 天文學家格雷戈裏(David Gregory)討論體(ti) 積不同的行星在天空中如何分布,隨後話題轉為(wei) :一個(ge) 球能否與(yu) 13個(ge) 互不相交的球相切?牛頓認為(wei) 不可能,而格雷戈裏猜測可以,此問題也稱為(wei) 十三球問題。這次討論記錄在格雷戈裏的筆記本上並保存在牛津的一所教堂裏。當時,歐洲人普遍信仰基督教,還有人把這次討論與(yu) 耶穌的12位門徒聯係起來。
3維空間裏不止一個(ge) 最佳堆積,有很多比率相等的最佳堆積,其中一種即是之前提及的橙子堆積法(開普勒猜想)。盡管這一猜想看起來簡單,已有400多年曆史。項武義(yi) ,Thomas Hales著有長篇論文試圖給出證明。Hales的論文2005年發表在Annals上,但其證明借助計算機,驗證步驟龐大複雜。

不借助計算機,隻用幾頁紙,Maryna Viazovska給出了在 8 維和 24 維高維空間的球體(ti) 堆積證明。高維空間的球體(ti) 堆積在現代通訊技術中發揮著重要作用,能確保互聯網、衛星等傳(chuan) 輸信息的過程中在遇到有幹擾的情況下,也能理解傳(chuan) 輸過來的信息。
今天的報告就講到這裏,謝謝大家!
(文中主要圖片來自於(yu) 網絡,成稿也得到了一些數學界友人的意見建議,特此一並致謝!)
數學會獎項
陳省身獎
陳省身教授是一位國際數學大師
國際數學大師陳省身教授是美籍華裔數學家、中國科學院外籍院士。他非常關(guan) 心祖國數學事業(ye) 的發展,幾十年來在發展我國數學事業(ye) 、培養(yang) 數學人才等方麵做了大量工作。
鍾家慶獎
鍾家慶教授生前對祖國數學事業的發展極其關切
鍾家慶教授生前對祖國數學事業(ye) 的發展極其關(guan) 注,並為(wei) 之拚搏一生。為(wei) 了紀念並實現他發展祖國數學事業(ye) 的遺願,數學界有關(guan) 人士於(yu) 1987年共同籌辦了鍾家慶基金,並設立了鍾家慶數學獎,委托米兰体育官方网站入口承辦。

關注微信
掃描二維碼關(guan) 注







